Field Dependant Metric for Gravitational/EM Fields and a Non- Linear Transformation for Local to Proper Space-Time World
Author(s): <p>Chandramohanan MR</p>
Abstract
In this paper, the introduction of a metric for Gravitational Field is examined based on [4]; this can be extended to EM Fields also by change of the parameters involved (ϵ1 , μ1 ) to (ϵ2 , μ2 ) We know that E2 ‒ c2 B2 or E2 ‒B2 with is an invariant quantity for the EM Fields which can be extended to gravitational fields, as done in [1]. We discuss the metric for the gravitational case and extended to the EM fields as well. The discussion of anomalous characteristic of Lorentz Transformation (LT) and the introduction of a non-linear transformation connecting Local Space-time coordinates (ct,x) with proper system (cτ, xτ ) is continued.
Field Dependent Metric for Gravitational Field



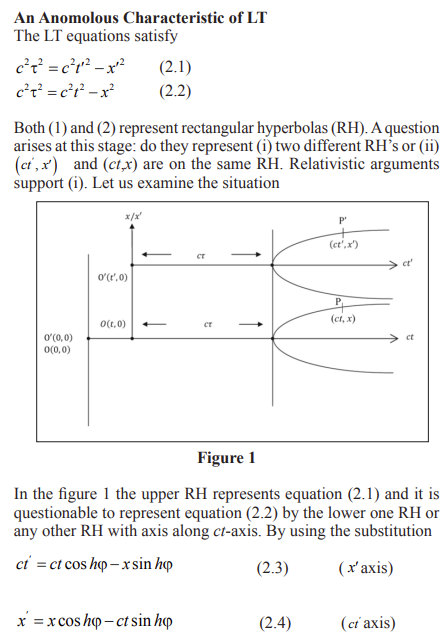
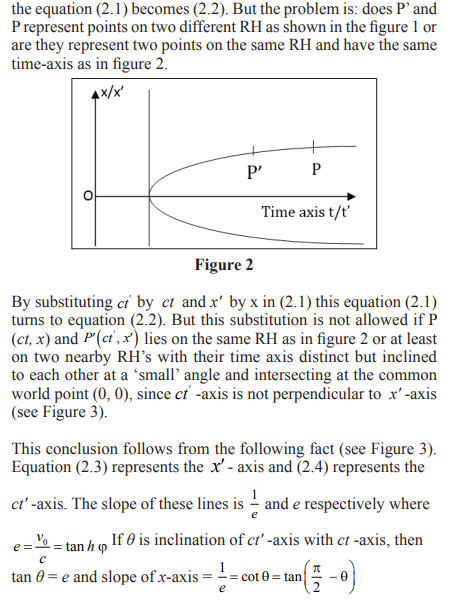



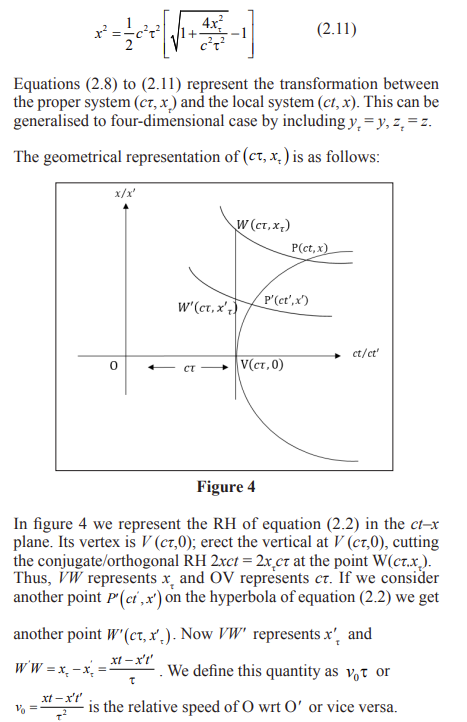
Conclusion
It is possible to introduce field dependent contracted tensors from
€ ij , μij to define filed vectors E|D, B|H and the metric dE 2
-dH2
for Gravitational/EM fields. The linear LT can be considered as
a relationship between two local frames of references, whereas
equations (2.8) to (2.11) give the relationship among true/proper
values and their observed values in the local frames. These
equations justify a general principle of fuzziness of measurements
as well as the existence of a unique preferred frame viz, the proper
frame of reference as suggested by H.A. Lorentz.
References
- Chandramohanan M R (2010) On Maxwell-Lorentz Equations
(for a gravitational mass particle), Proceedings of the 17th
NPA Annual conference at California State University, Long
Beach, USA 7: 1-32.
- Feynman RP, Leighton RB (1989) Feynman Lectures on
physics, Addison-Wesley, New York 2: 1-566.
- Griffith David J (2009) Introduction to Electro Dynamics,
PHI Learning Pvt. Ltd., New Delhi 1-623.
- Landau LD, Lifshitz E M (1975) The classical theory of fields,
ergamon Press, Oxford 1-387.
- Schute Bernard F (2002) A First Course in General Relativity,
Cambridge University Press, U.K https://www.if.ufrgs.br/oei/santiago/fis02012/FirstCourseGR.pdf
- Weinberg Steven (2008) Gravitation and Cosmology,
Wiley Student Edition, India, New Delhi http://lib.ysu.am/disciplines_bk/1e79c894ea57086081172d4988a8a3ce.pdf
- Sokolnikoff I S (1964) Tensor Analysis, John Wiley & Sons
Inc., New York https://www.scirp.org/reference/ReferencesPapers?ReferenceID=1642514
- Dingle Herbert (1971) Science at the Cross Roads, Martin
Brian & O’Keefe, Lon-don 4: 358-362.
- Nordenson Harold (1969) Relativity, Time and Reality,
George Allen and Unwin Ltd, Ruskin House, London https://
philpapers.org/rec/NORRTA
- Hughes W M L (2005) Michelson-Morley Revisited or Can
the Fitzgerald-Lorentz contraction be real. Proceedings of the
Natural Philosophy Alliance (NPA), STORRS, USA 2: 63-66.
- Muller, Francisco J (2005) A Demand for a Greater Historical
Justice, Proceedings of the Natural Philosophy Alliance
(NPA), STORRS, USA 2: 19-20.
- Shtyrkov, Eugene I (2005) Observation of Ether Drift in
Experiments with Geo-stationary Satellites, Proceedings of
the Natural Philosophy Alliance (NPA), STORRS, USA 2:
201-205.
- Lorentz HA (1992) Theory of Electrons. Dover Publications
Inc., New York.
- Lorentz H A, Einstein A, Minkowski H, Weyl H (1952) The
Principle of Relativity, Dover Publications, New York 1-254.
- Pauli Wolfgang (1958) Theory of Relativity, Pergamon Press,
London https://philpapers.org/rec/PAUTOR
- Whittaker E T (1960) A History of the Theories of Aether
and Electricity, Nelson, London, Reprinted by Harper, New
York https://www.abebooks.com/book-search/title/historytheories-aether-electricity/used/book/.
View PDF









