Journal of Engineering and Applied Sciences Technology

Introduction and Objectives The Fundamental Concepts

The determination of critical temperature (TC) in superconductors Type I and Type II is crucial for engineering, physics, and industrial applications. Along a series of articles and a book, 3D Interior Optimization mathematical methods were developed for modelling the classical-exponential BCS equation for Type I (TC) determination. Based on this model idea, a Molecular Effect Model (MEM) for Type II High Temperature Superconductors was primarily built up. For all of those mathematical models, 3D Interior and Graphical Optimization methods were applied. Results comprise a database of BCS and MEM (TC) values for Type I and Type II superconductors. Engineering and Physics applications are briefed. The challenges for future SC research are shown in Table 1, [Casesnoves, 2021, author’s proposal]. Some views in this field from electronics scientific community are explained in Table 2, [1]. The article has two main strands. Namely, the extended/complemented review of the conference presentation, set in simplified concepts, and the MEM new computational 3D modelling with 3D IO and 3D Graphical Optimization.

Table 1: Overview of possible future applications for SC and HTSC applications in transmission lines substitution/ improvements

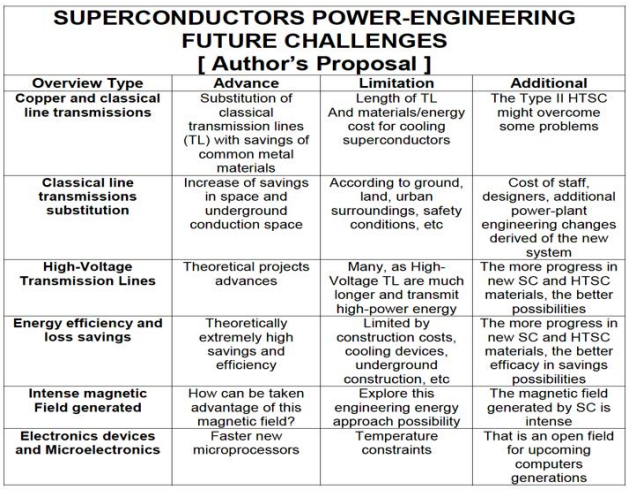
Table 2: Some future strategic research lines according [Basic research needs for superconductivity] criteria [1]. Note: that is an overview and brief resume with data of a prestigious institution among others

First Part: Brief of Review
The Basic Concepts

Previously, it was presented a condensed talk about a series of superconductors modelling contributions [2]. In short, the research in this field commenced with mathematical modelling of Isotope Effect, and continued with the creation of Molecular Effect Model (MEM), inspired in Isotope Effect ideas, but mathematically-modelling very different.

As it was explained at Conference presentation, this section is developed in as much as possible plain technical language, to be got easily. The most essential concepts in superconductors theory are simplified, as the IE and MEM principal ideas. Interior Optimization definition-concept reads,

Definition I: Interior-Graphical Optimization Method, [Casesnoves, 2018] is a type of Nonlinear Optimization that combines separation of variables method with stages of Graphical Optimization [Casesnoves, 2016], [Interior Graphical-Optimization Methods were created by Francisco Casesnoves on 3^rd November 2018, while he was preparing his Doctoral Thesis defence. First implementation of algorithms and computational-verification of simulations were carried out in the morning of April 1^st, 2020].

Figure 1 shows the very basic electrical current equation. Today, the resistance R can be considered a function of several variables. In superconducting materials it is function of an essential physical parameter: the temperature. A superconductor can be defined as any material type whose electrical resistance is approximately null under specific thermodynamic and electromagnetic conditions [3].

The superconductor material shows the physical-thermodynamical property of reducing the electrical resistivity (ρ), towards a zero magnitude order, however this is got approximately. The physics background reasons that cause the transition from common resistivity to superconducting low- resistivity when surpassing the critical temperature are mostly based on complex models in Quantum Mechanics and Molecular Chemistry, Tables 1-2 [1,3].

The usage of superconductors technology and future applications constitutes an open field in research with possible unpredictable achievements/purposes. A few current usages are: supercomputer laboratories whose power electrical demand is very high, medical devices that require to set high magnitude order magnetic fields (for example, Magnetic Resonance or Computarized Tomography), and Levitation Transport [1,3].

The Critical Temperature characterization in a superconducting material is essential for a unlimited number of reasons. Namely, optimal operation of the superconducting device, no matter what is its type, the energy precision calculations for superconducting manufacturing devices, their functioning safety requirements, the research of new superconducting materials starting from the recent achievements, the exact determination of diamagnetism and magnetic field interactions, and others. Therefore, the mathematical modelling of TC is essential for prediction of physical properties of any SC or HTSC material. The interaction with magnetic fields constitute other fundamental aspect of SC and HTSC.

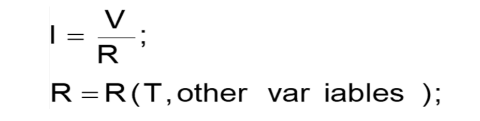
Figure 1: The fundamental electrical current equation. However, the resistance R can be considered a function of several variables. In superconducting materials it is function of an essential physical parameter: the critical temperature TC

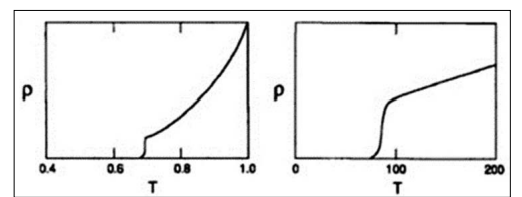
Figure 2: Resistivity as a function of temperature generalized for a Type I superconductor

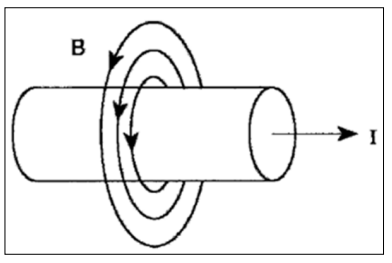
Figure 3: Very simple sketch showing the magnetic field created by a superconductor current or common electrical current

Interior Optimization (IO) Method Concrete Concepts

In the following, Figure 4, and Algorithms 1-2 show the basic concept of Interior Optimization. The method consists in carry out a multiple-optional optimization in a series of 3D charts, by selecting orderly the chosen magnitude values or constant figures at every step.

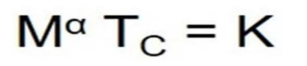
Figure 4: Fundamental Equation of Isotope Effect (IE)

Algorithm 1: Basic Algorithm of a function of several variables for computational implementation

Algorithm 2: Simplification of Inverse Method Optimization for IE with constraints

First BCS IO Model Results (I) Example

The IO model for Isotope Effect is shown for the classical SC Hg. Figures 5-9 presents the graphical stages and the numerical corresponding results and Algorithm 3 details the formula implemented. Figures 5, 6 show the first and the second stages. BCS isotope effect model: this simple Hg model works for type I superconductors. Namely, Hg (Type I) example in two 3D stages:

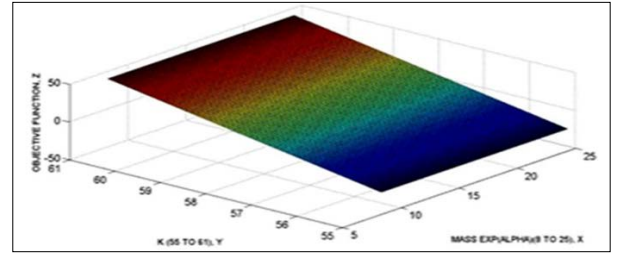
Figure 5: The fundamental first stage for Hg. At X-Y plane, Mass x ( exp (alpha) ), and K . At Z the objective function. Algorithm 3

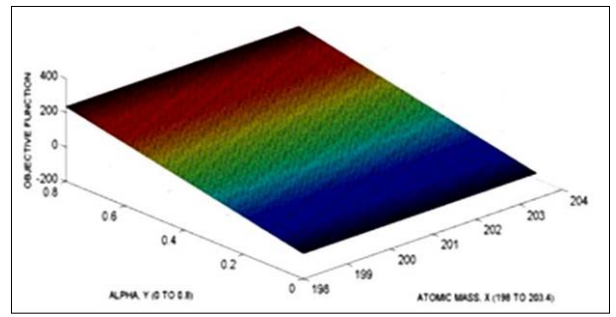
Figure 6: The second stage for Hg. At X-Y plane, Alpha, and Atomic Mass. At Z the objective function. Algorithm 3

Algorithm 3: Inverse Method Optimization for IE with constraints

First BCS Model IO Results (II)

The results for the IO optimization are shown, Figures 7-9. Figures 7, 9 detail the numerical precision reached. In other words, BCS Isotope Effect model works in this simple model for Type I superconductors Hg example in two 3D stages: 1) K and Mα TC; 2) M and α.

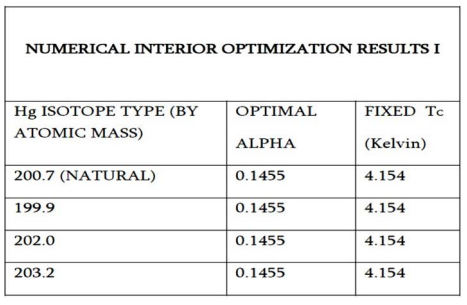
Figure 7: In superconducting materials Type I, Hg numerical results at first and second stages

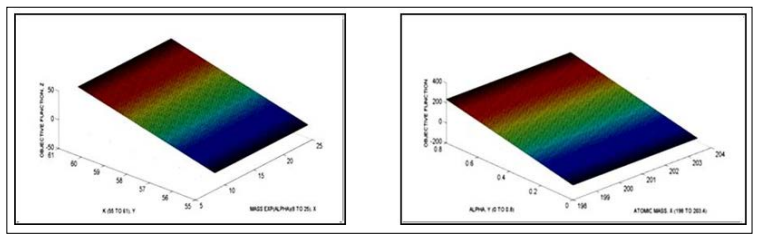
Figure 8: The first and second stage for Hg. At X-Y plane, Alpha, and Atomic Mass. At Z the objective function, Algorithm 3

First stage Interior Optimization Results

The first stage of Hg IO results are shown in Figures 7, 8, 9. Figure 7 shows optimal values for every isotope, alpha and TC. Figure 8 shows the two subsequent phases. Figure 9 presents the optimal numerical figures for K and the residuals. Results match the literature published datasets.

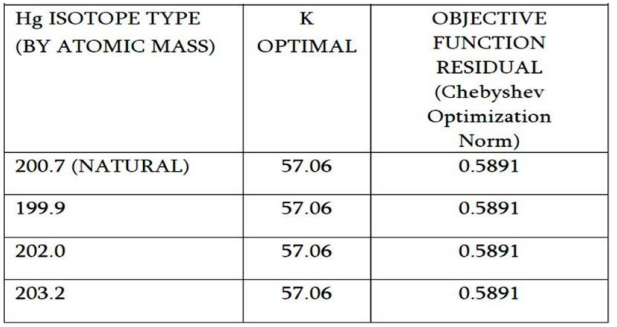
Figure 9: In superconducting materials Type I, Hg numerical results at first and second stages

Dual-IO BCS Model Results Example (Pt and Sn)

After the IO applied for one classical superconductor, Hg, a Dual optimization was performed for two elements whose atomic masses (UAM) are similar. Namely, Pt and Sn. The stages were three, Figures 10-13. The parameters optimized at every stage are detailed in Figure 11. The distribution of parameters for every stage are set at X and Y axes in Figures 10, 12, 13. Residuals are low.

Multiobjective-IO BCS Model Results Example (Mo + Ti + Zn) The following publication as detailed in Proceedings was a Multiobjective one. Namely, (Mo + Ti + Zn). Figures 14-18 show the IO stages, numerical results, and method brief.

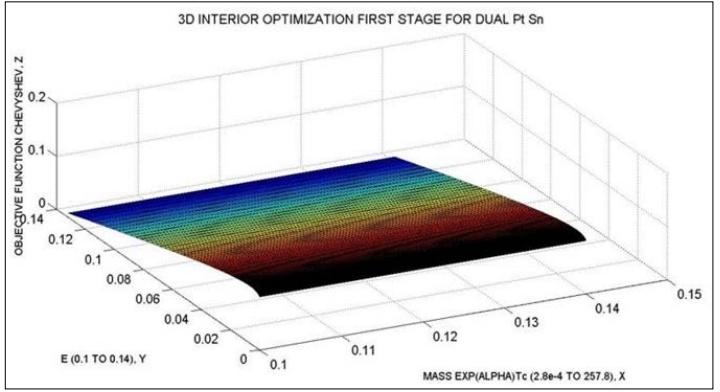
Figure 10: The first stage for Pt and Sn Dual Optimization. At X-Y plane, E (K) and Mass x Exp (Alpha) x TC. At Z the objective function, Algorithm 3

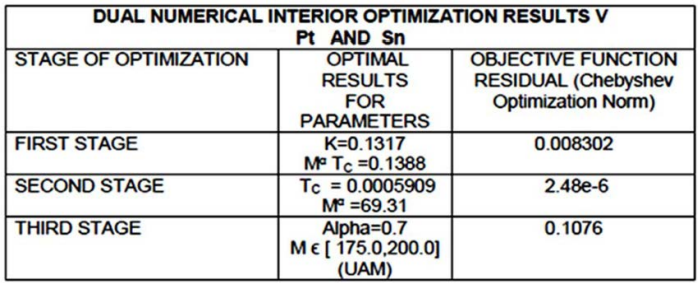
Figure 11: The Stages Numerical Results for Pt and Sn Dual Optimization

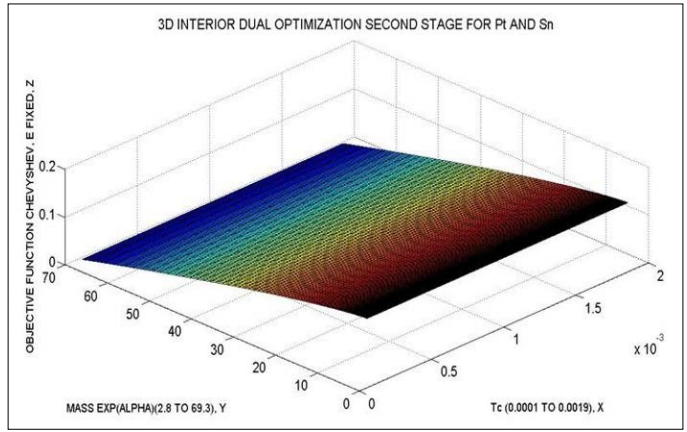
Figure 12: The second stage for Pt and Sn Dual Optimization. At X-Y plane, Mass x Exp (Alpha), and TC. At Z the objective function, Algorithm 3

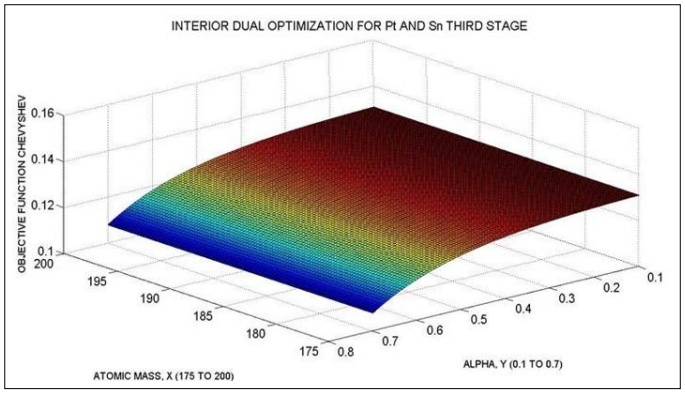
Figure 13: The third stage for Pt and Sn Dual Optimization. At X-Y plane, Atomic Mass, and (Alpha). At Z the objective function, Algorithm 3

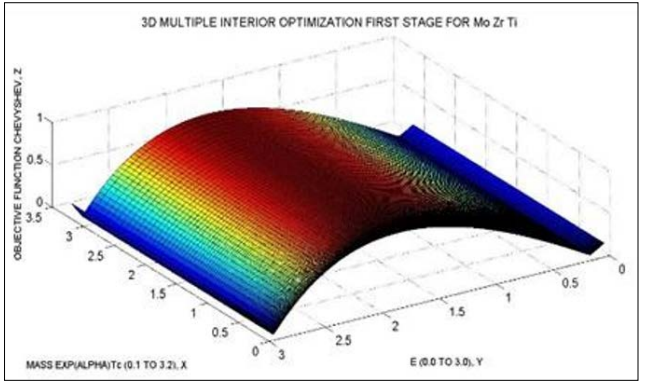
Figure 14: The first stage for (Mo + Ti + Zn) Multiobjective Optimization. At X-Y plane, E (K) and Mass x Exp (Alpha) x TC. At Z the objective function, Algorithm 3

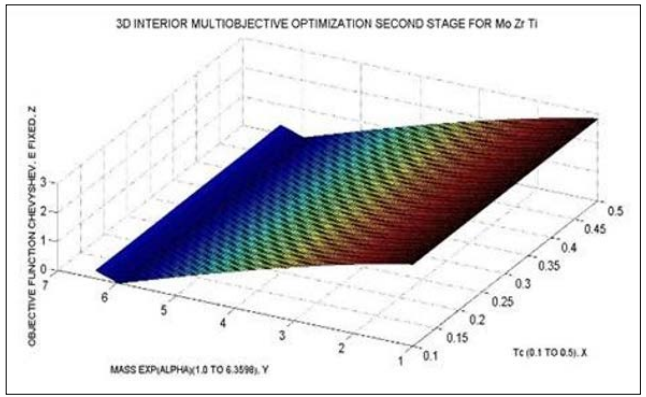
Figure 15: The second stage for (Mo + Ti + Zn) Multiobjective Optimization. At X-Y plane, Mass x Exp (Alpha), and TC. At Z the objective function, Algorithm 3

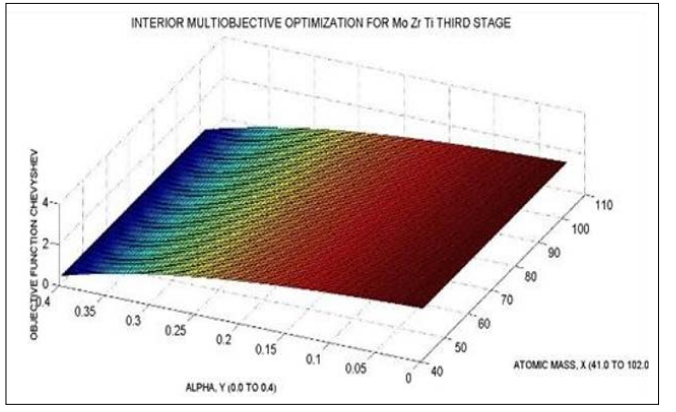
Figure 16: The third stage for (Mo + Ti + Zn) Multiobjective Optimization. At X-Y plane, Atomic Mass, and (Alpha). At Z the objective function, Algorithm 3 equal. The HTSCs class for this software graphical optimization is [Tl- Sn-Pb-Ba-Si-Mn-Mg-Cu-O]. Molecular HTSC Group Numerical example coincidence between experimental and MEM data is marked

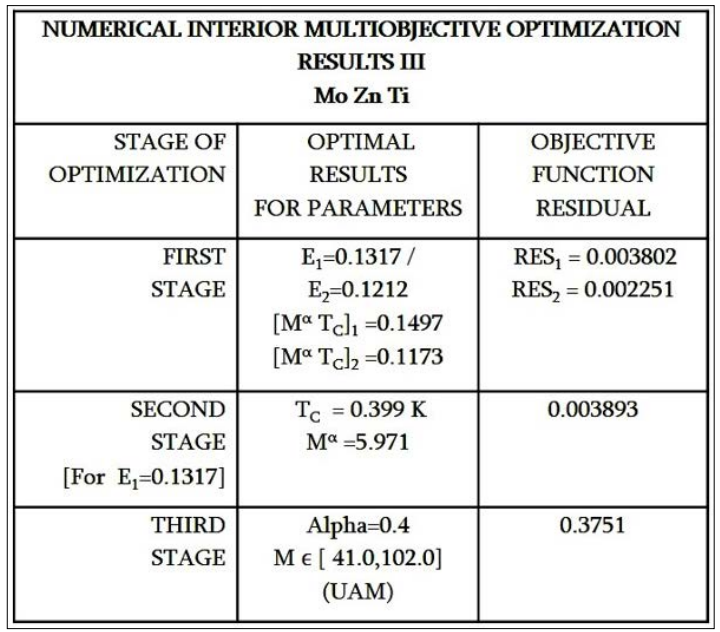
Figure 17: Numerical results for (Mo + Ti + Zn) Multiobjective Optimization

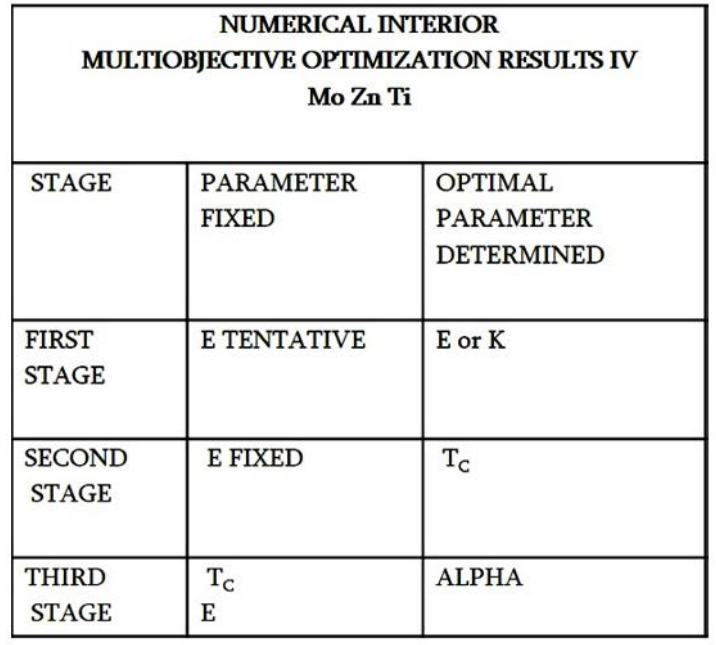
Figure 18: Brief of Stages Interior Optimization method for (Mo + Ti + Zn) Multiobjective Optimization

Molecular Effect IO Model Results Example (I) (Thallium Compounds, Type II, High Temperature Superconductors, HTSC)

The MEM results for Thallium compounds Type II superconductors [Tl-Sn-Pb-Ba-Si-Mn-Mg-Cu-O] are shown in Figures 19-21.

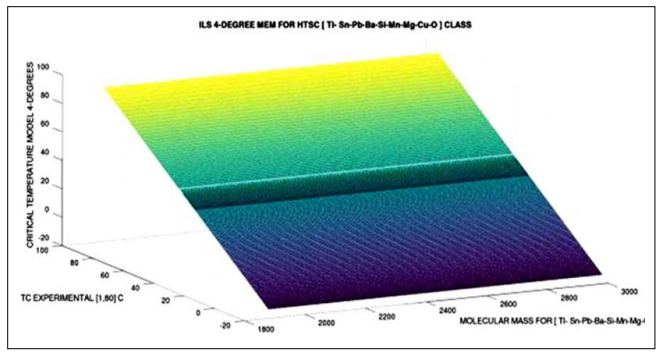
Figure 19: 3-Degree polynomial MEM 3D graph showing model TC prediction and 3D experimental data which are approximately

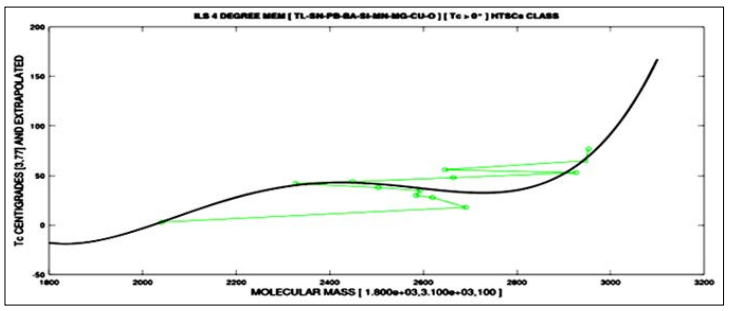
Figure 20: 3-Degree polynomial fitting for optimization of [Tl- Sn-Pb-Ba-Si-Mn-Mg-Cu-O] MEM

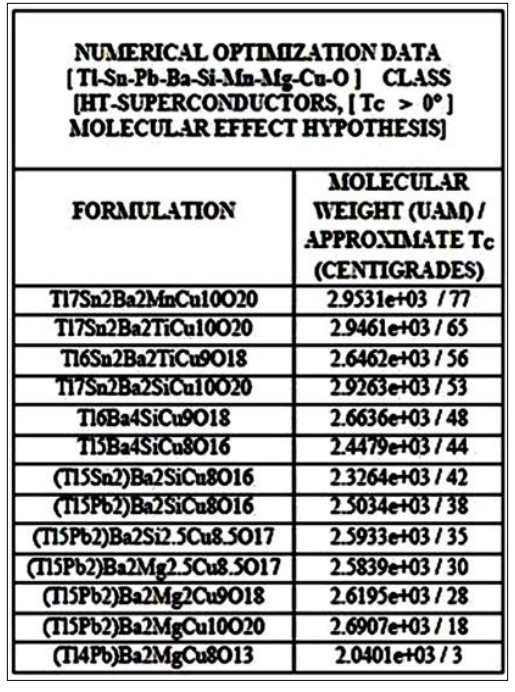
Figure 21: The fundamental experimental data implemented in MEM for Thallium compounds Type II superconductors

Molecular Effect IO Model Results Example (II). (Hg- CUPRATES Type II HTSC)

Hg-Cuprates Type II HTSC MEM is the most accurate at present research. artificial Intelligence Optimal MEM sector for Hg- Cuprates HTSCs class. Generations Number is 300. Green arrow zone, the almost exact fit, red arrow, inset, shows the approximately acceptable fit. Hg-Cuprates MEM shows be the best at this stage. Model fits approximately well between molecular weights interval [500, 1400] for all values of TC. Figures 22, 24-28.

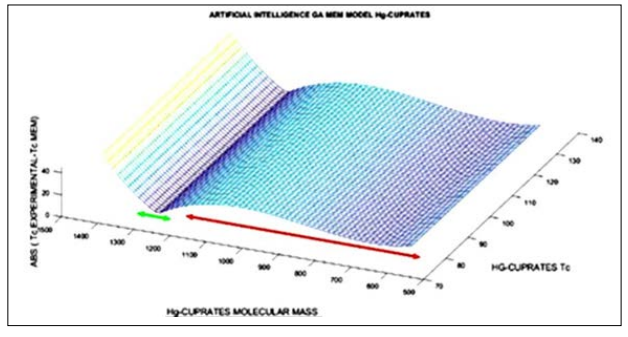
Figure 22: Artificial Intelligence Optimal MEM sector for Hg- Cuprates HTSCs class. Generations Number is 300. Green arrow zone, the almost exact fit, red arrow, inset, shows the approximately acceptable fit. Hg-Cuprates MEM shows be the best at this stage. Model fits approximately well between molecular weights interval [500, 1400] for all values of TC

Superconducting Multifunctional Transmission Line (Hypothesis)

This SCMTL line has capability to transmit electrical power at a wide range of temperatures, depending on the engineering resources and power energy demand. The energy demands at industrial countries and increased electrical power use has increasing prospective use for future. Both for electrical power transmission and electromagnetic waves TLs energy losses represent a severe difficulty for operational/economical optimization. Minimization of the electrical resistance is an optimal possible method to avoid electrical power loss transmission lines diminution. HTSCs and standard superconductors materials could work out that hurdle. If the engineering design/operative-functionality perform properly. In addition, the HTSCs and superconducting materials manufacturing/maintenance costs should be moderate.

Figure 23: Primary fundamental applications of SCMTLs. Just remark that those are primary applications

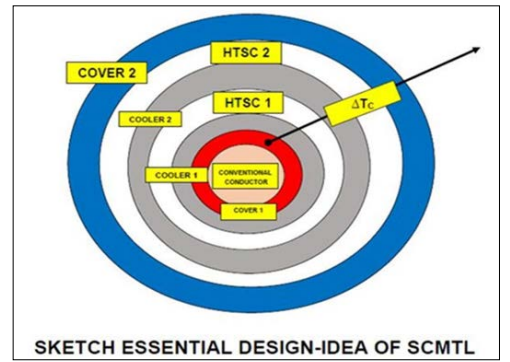
Figure 24: Basic design of a SCMTL. HTSC1, first superconductor type, HTSC2 the second one with higher TC. Direction of TC increase [arrow] marked with arrow. Conventional conductor at center. This is a simple idea-design

Second Part: Mathematical And Computational Methods The starting point requires to set the concept of Interior-Graphical Optimization as follows,

Definition I: Interior-Graphical Optimization Method, [Casesnoves, 2018] is a type of Nonlinear Optimization that combines separation of variables method with stages of Graphical Optimization [Casesnoves, 2016], [Interior Graphical-Optimization Methods were created by Francisco Casesnoves on 3^rd November 2018, while he was preparing his Doctoral Thesis defence. First implementation of algorithms and computational-verification of simulations were carried out in the morning of April 1^st, 2020].

The objective of this continuing study is to apply 3D Interior and Graphical Optimization for modelling of Hg-Cuprates, [Hg-Ba- Ca-Cu-O] constrained to [TC > 0° K]. The methods applied are 2D/3D Graphical Optimization and Genetic Algorithm techniques software database from. All the software developed constitutes improvements/applications of previous research publications, not limited to Superconductors field [2,3,4-10].

Along the GA optimization series published, Evolutionary Algorithms have proven be accurate and practical, with many programming options [48,50]. Given any HTSCs class, if differences of molecular weight as a result of proportion/isotopic- variation in the molecule occur, the MEM, may constitute an hypothesis to approximate/predict the TC magnitude changes may be useful/efficacious, Figures 22-28. MEM was initially conceived related on the basis of classical largely proven Isotope Effect. Inverse Methods, could also be applied to select a desired TC with optimal molecular weight composition in MEM [2,3,4-10]. The innovations of this second part-following research are given by the software for 3D IO-Graphical Optimization methods. As was presented in, the advance consists in setting at Z axis the absolute difference between MEM TC and experimental TC [2,3]. The software method applied in this study is set with 3D IO-Graphical Optimization Imaging Processing programming. Results involve, Figures 25-28, improved MEM for Hg-Cuprates, both in 3D and polynomial 3, 5 degrees fittings. In other words, further more precise TC 2D polynomial and 3D imaging-processing predictive equations, Figures 27,28.

The objective is to continue the improvements for MEM in search for refinements and precision. Applications in Electronics Physics new materials are explained in Tables 1,2. At Table 3, the software programming setting data implemented for algorithms 1,2,3 (modified). For these equations the programming patterns are made based on [4-6,2,3]. The Tikhonov Functional is implemented/improved with Chebyshev L1 norm from previous research [2-3]. As in the difference with previous publications is the setting of MEM algorithm objective function at Z axis [abs (TC Experimental- TC MEM]), Figures 25-28 [3].

For these Hg-Cuprates, first stage method, Figures 27-28, comprises the polynomial fitting to obtain approximations for imaging-processing programming constraints. Second stage is direct application of these polynomial equations to get 3D Interior and Graphical Optimization charts. The refinements and decrease of errors compared to Figure 22 to obtain the MEM improved optimal model sectors are got.

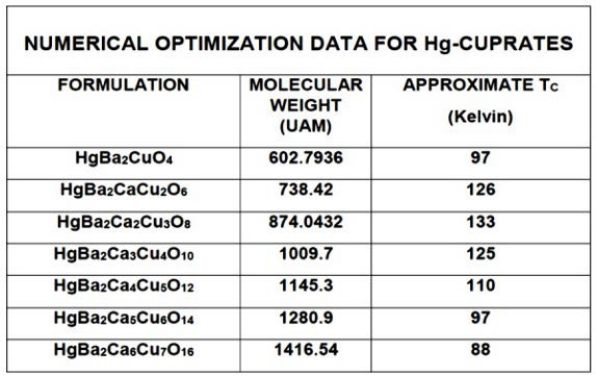
Table 3: Numerical Data for Cr and HTSC Hg-Cuprates. Note the 97 Kelvin temperature corresponds to two different compounds. This fact gives to the 2D and 3D MEM plots a parabolic-like analytic geometry shape. Hg-Cuprates TC is expressed in Kelvin usually

Results

The results of the Hg-Cuprates group of HTSC are presented in 2D polynomial MEM fit and 3D Graphical Optimization graphics, based on [ref universal]. This Type II group is the one that shows better appropriateness with the MEM polynomial model. The model shown on the conference has been improved in precision both in 2D and 3D, Figures 26-28.

The computational method applied was to refine the model equation with implementation of the residuals of the polynomial fitting. This improved the accuracy of the error range in the 3D Graphical Optimization of the MEM Hg-Cuprates model. Therefore, it is shown, Figures 26-28 the improved 3D Inverse and Graphical Optimization, the prediction of TC can be guessed along the zones where the error belongs to interval ≈ [0, 5] K, Figures 26-28 present the polynomial fitness, in 3 degrees and in 5 degrees with accurate agreement for the polynomial model.

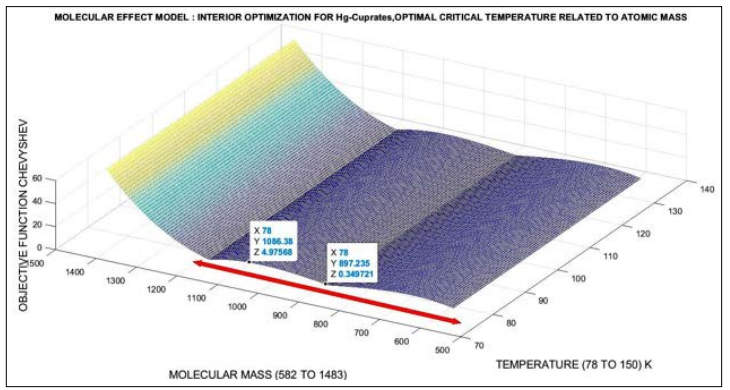
Figure 25: The 3D improved optimization for MEM Hg-Cuprates with an interval (red arrow) with error ≈ [0, 5] K. Although the error should be about a minimum of 10^-1, it can be considered an improvement compared to Figure 22

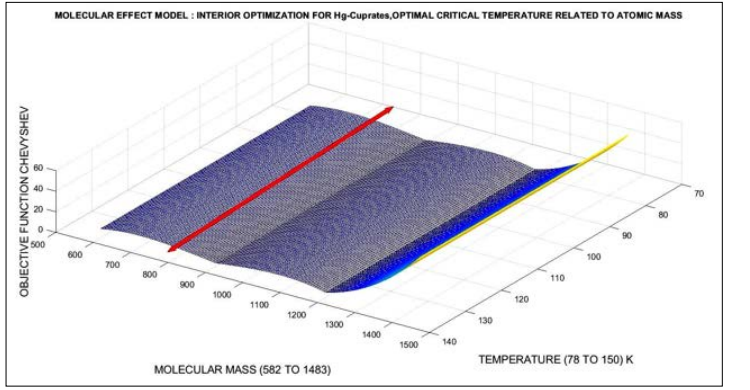
Figure 26: The 3D improved optimization for MEM Hg-Cuprates with an interval (red arrow) of low error interval for the whole temperature range. Although the error should be lower, it can be considered an improvement compared to Figure 22

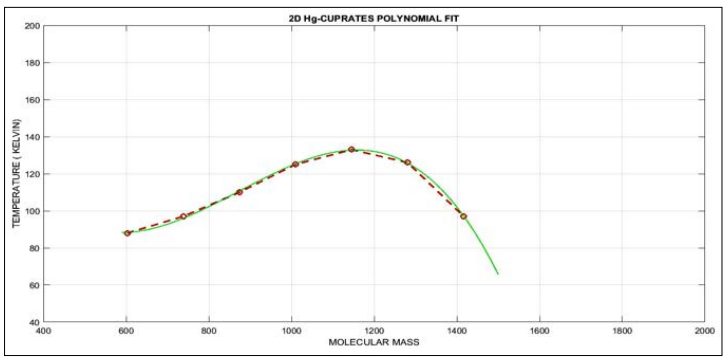
Figure 27: The 2D improved 3-degree polynomial MEM optimization for Hg-Cuprates showing a parabolic quasi-shape curve with accuracy between model (green) and experimental data (red). Although the polynomial error is low, when passing on to 3D MEM predictions it increases

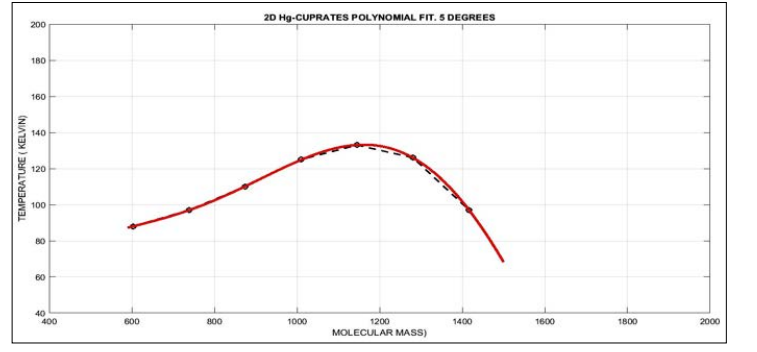
Figure 28: The 2D improved 5-degree polynomial MEM optimization for Hg-Cuprates showing a parabolic quasi-shape curve with accuracy between model (red) and experimental data (black). Although the polynomial error is low, when passing on to 3D MEM predictions it increases. The fitting is slightly better than the 3-degree polynomial

Physics and Engineering Applications

Applications of SC and HTSC is an open and fruitful field for Physics, materials Physics, Quantum Mechanics, Chemistry, and other science branches. These can be guessed and not limited to the topics shown in Tables 1, 2. Further applications details can be read in series of previous publications, for instance [2,3,4,5,11].

Discussion and Conclusions

The objective of the study was double, namely, to review with additional explanations the conference presentation, and secondly to improve computationally-numerically the Hg- Cuprates MEM model. Additionally, a number of applications of Type I and Type II semiconductors modelling are also explained with future investigation lines, Tables 1-2.

A number of figures have been explained in the review part, with learning clarifications about formulas and datasets, Figures 1-24. The part of MEM Hg-Cuprates MEM shows a better precision in the model with a diminution of error ≈ [0, 5] K for almost all molecular weights.

The computational software developed had two main steps. The first program was a polynomial fitting to get a tentative numerical boundaries for the 3D IO and Graphical Optimization imaging- processing software. However, next research objective should get results with errors about 10^-1 as minimum.

In summary, an extended resume of a conference paper was presented firstly. Secondly, a MEM model computational implementation for Hg-Cuprates was demonstrated with 3D and 2D IO and Graphical Optimization imaging-series. Applications of semiconductors modelling are also explained with future investigation lines, Tables 1-2.

Scientific Ethics Standards

Important remarks: images and table-data reminders from previous contributions are intended for explicit improved understanding. This study contains improved programming, [Casesnoves, May 7^th, 2024], and engineered software that was developed for numerical Hg-Cuprates imaging-processing database, Second Part. Formulas applied/included are from previous publications. Graphical Optimization Methods were created by Dr Francisco Casesnoves in 3^rd November 2016, and Interior Optimization Methods in 2019. This article has previous papers information, whose inclusion is essential to make the contribution understandable. This study was carried out, and their contents are done according to the International Scientific Community and European Union Technology and Science Ethics.

References: ‘European Textbook on Ethics in Research’. European Commission, Directorate-General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN. And based on ‘The European Code of Conduct for Research Integrity’. Revised Edition. ALLEA. 2017. This research was completely done by the author, the computational-software, calculations, images, mathematical propositions and statements, reference citations, and text is original for the author. When a mathematical statement, algorithm, proposition or theorem is presented, demonstration is always included. When a formula is presented, all parameters are detailed or referred. If any results inconsistency is found after publication, it is clarified in subsequent contributions. When a citation such as [Casesnoves, ‘year’] is set, it is exclusively to clarify intellectual property at current times, without intention to brag. The article is exclusively scientific, without any commercial, institutional, academic, any religious, religious-similar, non-scientific theories, personal opinions, political ideas, or economical influences. When anything is taken from a source, it is adequately recognized, or put a number in a remark. Ideas and some text expressions/sentences from previous publications were emphasized due to a clarification aim. Number of references is large to provide literature in open access for public health care institutions.

References

1. Sarrao J, Nault R, Kwok WK, Bozovic I, Mazin I, et al. (2006) Basic research needs for Report on the Basic Energy Sciences Workshop on Superconductivity https://www.osti.gov/biblio/899129.
2. Casesnoves F (2023) Superconducting materials critical temperature models designed with 3D interior Optimization Scientific talk and Proceedings Conference. Invited Talk at 3rd Global Summit on Graphene and 2D Materials (2DMAT2023) held Virtually on August 24-25.
3. Casesnoves F (2022) Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors. Standards 2: 430-448.
4. Casesnoves F (2020) Advanced Interior Optimization Methods with Electronics Int. J. Sci. Res. Sci. Eng. Technol 7: 97-110.
5. Casesnoves F (2020) Multiobjective Interior Optimization Computational Methods for Electronics BCS Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol 6: 280-293.
6. Plakida N (2010) High-Temperature Cuprate Superconductors Experiment, Theory, and In Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany 10-500.
7. Alexandrev AS (2003) Theory of Superconductivity, from Weak to Strong Coupling. Series in Condensed Matter Physics; Institute of Physics Publishing 1-300.
8. Khare N (2003) Handbook of High-Temperature Marcel Dekker: New York, NY, USA https:// libcat.colorado.edu/Record/b3542430?sid=7688624.
9. Buschow K (2003) Magnetic & Superconducting Materials, 2nd ed. Elsevier: Amsterdam, The Netherlands.
10. Seidel P (2015) Applied Superconductivity. Wiley-VCH: Hoboken, NJ, USA https://wiley-vch.de/en/areas-interest/engineering/electrical-electronics-engineering-10ee/ electronic-materials-10eeb/superconductors-10eeb2/applied- superconductivity-978-3-527-41209-9.
11. Casesnoves F (2020) Interior Optimization Methods with Electronics Int. J. Sci. Res. Sci. Eng. Technol 7: 428-436.
12. Vora AM (2008) Modified Transition Temperature Equation for Superconductors. Chin. Phys. Lett. 25: 2162.
13. Drechsler S, Mishonov T (1998) High-T C Superconductors and Related Materials Material Science, Fundamental Properties, and Some Future Electronic Springer Science Media: Berlin/Heidenberg, Germany.
14. Kazufumi I, Bangti J (2015) Inverse Problems, Tikhonov Theory and Algorithms. Series on Applied Mathematics; World Scientific: Singapore 22.
15. Casesnoves F (2018) Mathematical Models and Optimization of Erosion and Ph.D. Thesis, Taltech University, Tallinn, Estonia https://digikogu.taltech.ee/et/item/53c43f0d-98ea-4e92-ab4c-c020dc316ff1.
16. Casesnoves F (2019) The Numerical Reuleaux Method Computational and Dynamic Basics with Applications (First Part). Sciencia Scripts: Chisinau, Moldova.
17. Casesnoves F (2018) Primary Modelling for Electromagnetic Waves Transmission in Extreme Weather Int. J. Innov. Res. Sci. Eng. Technol 7: 10294-10300.
18. Casesnoves F (2019) The Numerical Reuleaux Method, a Computational and Dynamical Base with First Part; Lambert Academic Publishing: Saarland, Germany ISBN 103659917478.
19. Darwin C (2004) The Origin of Species. Barnes & Noble Classics: New York, NY, USA https://www.barnesandnoble.com/w/the-origin-of-species-charles-darwin/1116788568.
20. Haupt R, Haupt S (2004) Practical Genetic Algorithms, 2nd ; Wiley: New York, NY, USA https://www.wiley.com/en-us/l+Genetic+Algorithms%2C+2nd+Edition-p-9780471671756.
21. Abramowitz M, Stegun IA (1964) Handbook of Mathematical Functions; U.S. Government Printing Office: Champaign, IL, USA 55.
22. Casesnoves F, Suzenkov A (2017) Mathematical Models in Biotribology with 2D-3D Erosion Integral-Differential Model and Computational-Optimization/Simulation Programming. J. Sci. Res. Comput. Sci. Eng. Inf. Technol 2: 329-356.
23. Casesnoves F, Antonov M, Kulou P (2016) Mathematical models for erosion and corrosion in power A review of applicable modelling optimization techniques. 7th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia 1-11.
24. Casesnoves F (2018) 2D computational-numerical hardness comparison between Fe- based hardfaces with WC-Co reinforcements for Integral-Differential Key Eng. Mater J 762: 330-338.
25. Casesnoves F, Surzhenkov A (2017) Inverse methods for computational simulations and optimization of erosion models in power In Proceedings of the RUTCON2017 Power Engineering Conference, Riga, Latvia 1-8.
26. Casesnoves F (2012) Computational Simulations of Vertebral Body for Optimal Instrumentation J. Med. Devices 6: 021014.
27. Casesnoves F (2007) Large-Scale Matlab Optimization Toolbox (MOT) Computing Methods in Radiotherapy Inverse Treatment In High Performance Computing Meeting; Nottingham University: Nottingham, UK.
28. Casesnoves F (2007) A Monte-Carlo Optimization method for the movement analysis of pseudo-rigid In Proceedings of the 10th SIAM Conference in Geometric Design and Computing, San Antonio, TX, USA.
29. Casesnoves F (2013) Applied Inverse Methods for Deformable Solid Dynamics/Kinematics in Numerical Reuleaux Method (NRM). Int. J. Numer. Methods Appl. 9: 109-131.
30. Casesnoves F (2018) Nonlinear comparative optimization for biomaterials wear in artificial implants technology. In Proceedings of the Applied Chemistry and Materials Science RTU2018 Conference Proceedings, Rajasthan Technical University, Kota, India 800: 52-59.
31. Allison J, Amako K, Apotolakis J, Araujo H, Dubois PA, et al. (2006) Geant4 Developments and Applications. IEEE Trans. Nucl. Sci 53: 270-278.
32. Batic M, Hoff G, Pia MG, Saracco P, Weidenspointner G (2013) The Geant4 Simulation Toolkit. IEEE Sci. Symp. Med. Imaging Conf. Seoul 60: 2934-2957.
33. Luenberger GD (2008) Linear and Nonlinear Programming, 4th ed. Springer: Berlin/Heidelberg, Germany https://warin.ca/ressources/books/2016_Book_pdf.
34. Huang X (2011) Does the isotope effect of mercury support the BCS theory. arXiv:1102.1467.
35. Hummel RE (2011) Electronic Properties of Materials; Springer: New York, NY, USA https://link.springer.com/book/10.1007/978-1-4419-8164-6.
36. Kasap F, Capper P (2000) Springer Handbook of Electronic and Photonic Materials, 4th ed. Springer: Berlin/ Heidelberg, Germany https://download.e-bookshelf.de/download/0000/0009/24/L-G-0000000924-0002340205.pdf.
37. Kessel W (1974) On a General Formula for the Transition Temperature of Naturforschung 29a: 445- 451.
38. Kulou P, Casesnoves F, Simson T, Tarbe R (2017) Prediction of abrasive impact wear of composite hardfacings. Solid State Phenomena. In Proceedings of 26th International Baltic Conference on Materials Engineering; Trans Tech Publications: Bäch, Switzerland 267: 201-206.
39. Luiz A (2010) Superconductivity-Theory and InTechOpen: London, UK ISBN 9789533071510.
40. Reynolds CA, Serin B, Nesbitt LB (1951) The Isotope Effect in Superconductivity. I. Mercury. Phys. Rev 84: 691.
41. Seri B, Reynolds CA, Nesbitt LB (1950) Mass Dependence of the Superconducting Transition Temperature of Letters to Editor. Phys. Rev 80: 761.
42. Todinov M (2005) Reliability and Risk Models; Wiley: New York, NY, USA https://wiley.com/en-us/+and+Risk+M odels%3A+Setting+Reliability+Requirements%2C+2nd+Ed ition-p-9781118873199.
43. Vidyasagar M (1993) Nonlinear Systems Analysis, 2nd ; Prentice Hall: Hoboken, NJ, USA http://www.coep.ufrj. br/~liu/livros/Nonlinear%20systems%20analysis%20-%20 M.%20Vidyasagar.pdf.
44. Wesche R (2017) Chapter 50. High-Temperature Superconductors. In Springer Handbook of Electronic and Photonic Materials; Springer: Berlin/Heidelberg, Germany https://www.springerprofessional.de/en/high-temperature-superconductors/15108400.
45. Parinov I (2017) Microstructure and Properties of High- Temperature Superconductors, 2nd ed. Springer: Berlin/ Heidelberg, Germany ISBN: 978-3-642-34440-4.
46. Fossheim K, Sudbø A (2004) Superconductivity Physics and    Wiley:  New  York, N Y, US A https ://ww w.wiley.com/en-cn/uctivity%3A+Physics+and+Applications-p-9780470026434.
47. Wang Y (2013) Fundamental Elements of Applied Superconductivity in Electrical Engineering. Wiley: New York, NY, USA.
48. European Textbook on Ethics in Research (2021) European Commission, Directorate- General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN https://op.europa.eu/en/publicationdetail/-/publication/12567a07-6beb-4998-95cd-8bca103fcf43.
49. ALLEA (2017) The European Code of Conduct for Research Integrity, Revised ALLEA: Bern, Switzerland https://allea.org/code-of-conduct/.
50. Swedish Research Council (2017) Good Research Swedish Research Council: Stockholm, Sweden https://wwwvr.se/english/analysis/reports/our-reports/2017-08-31-good- research-practice.html..