Journal of Engineering and Applied Sciences Technology

Introduction

For the speed of light, both Newton’s classical mechanics and Einstein’s theory of relativity presuppose one premise each, which can be seen clearly in chapter 2 of Stephen Hawking’s book A Brief History of Time, “Space and Time”, see Figure 1 [1-4].

Figure 1: Description of the premises presupposed by classical mechanics and relativity in Hawking’s “A Brief History of Time”.

It is easy to notice that in the passage marked by the red line in Figure 1, both theories have a common assumption in their premises, namely, “but will not always agree on how far the light traveled” in Newton’s theory and “however, do not agree on the distance the light has traveled” in the premise of relativity theory, and this same assumption is exactly what this paper is going to explore and point out. It is a subjectively correct and objectively wrong assumption.

Interpretation

To illustrate this, assume here that there are two inertial objects P and Q moving relative to each other, where Q is stationary at position c of some reference system, and P emits a light pulse at the moment of moving to position a of this reference system. When Q at point c receives this light pulse, P has already moved to position b. Then, according to the common view of today’s physicists such as Newton and Einstein, the distance traveled by light during this process is ac for Q and bc for P, as shown in Figure 2. On this basis, the difference between the two is that Newton’s theory holds that different observers of this process will not disagree on the time taken by light, and therefore the speed of light propagation will be inconsistent for different observers; while relativity theory, based on Michelson’s interference experiment, holds that different observers will have inconsistent views on the time taken by light under the premise of affirming the constant speed of light [5-7].

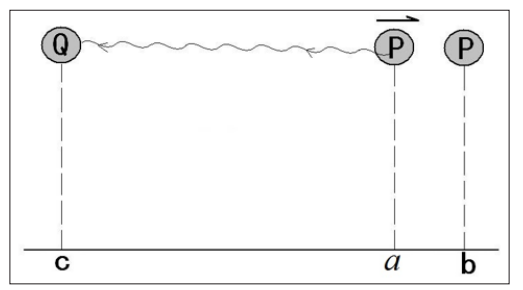
Figure 2: Spatial distance traveled by an optical pulse during its emission from one place in space to another

However, a key question here is what makes us think that the distance traveled by light in this process is inconsistent for the two references in the first place? Is it by subjective perception or objective reasoning? Because objectively, the propagation of light differs from the motion of particles or other objects in that, the speed of light propagation is relative to “space”, and this “space” is not predetermined in terms of which frame of reference is the stationary 3-dimensional space! In other words, although P is moving with respect to Q, it does not mean that P is also moving with respect to “space”. Moreover, even if P appears to be moving in space to a stationary Q, this is only from the perspective of Q in a 3-dimensional space. If Q is standing in a higher 3-dimensional space, then we usually think that the relative motion of P and Q is only the motion of their respective solid parts in the same 3-dimensional space, but the actual situation is that P is in a 3-dimensional “space” and Q is in another 3-dimensional “space “ are in relative motion in a higher dimensional space of 4 or more dimensions. Therefore, when P moves to the position point a of the reference system where Q is located, we do not take it for granted that P is at the position of point a at this instant, but at any instant P is always at some position a’ in another 3-dimensional “space” where the whole body is moving relative to Q, as shown in Figure 3. This also means that when P moves to the position of point a and emits a light pulse, this light is not emitted from the position a of the stationary frame of reference where Q is located, but from the position a’ of the stationary frame of reference where P is located. Moreover, when Q receives the light pulse, the light propagates between the two objects not over a distance in 3 dimensions with Q as the rest system, but over a distance in higher dimensions with the whole universe as the background! This distance, even if it varies with time, is independent of the choice of coordinate system, it should be the same for any observer or reference system, i.e., the spatial distance traveled by the light in the process should be bc for either P or Q!

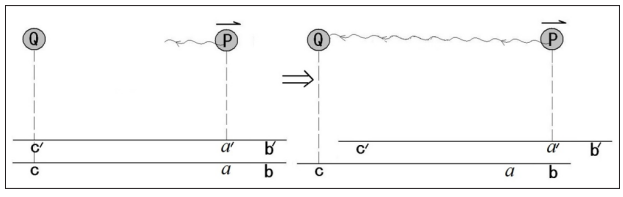
Figure 3: Spatial distance traveled by an optical pulse during its emission from one place in space to another

If we assume that the 3-dimensional space where Q is located and the other 3-dimensional space where P is located relative to Q’s motion are viewed as two parallel 2-dimensional planes, then it is not difficult to understand that when P moves to the position of point a in the 3-dimensional space where Q is located, this position is actually the projected position of P, as shown in Figure 4. Obviously, for Q, the actual position of P is actually not represented by the conventionally understood 3-dimensional coordinates, but rather by higher dimensional coordinates of 4 dimensions or more!

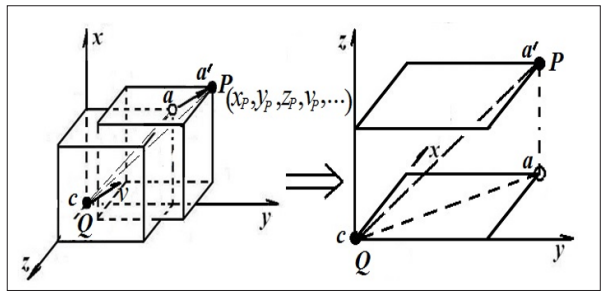
Figure 4: The actual spatial location of the inertially moving object when it emits a signal.

The next question is, can there be experiments to confirm this principle? We can actually easily associate that it can be verified by current GNSS measurement experiments: that is, assuming a 3-dimensional right-angle coordinate system “ o-xyz “ with the Earth as the stationary reference system with the geocenter “ o “ as the origin, and ground time “ t “ as the timekeeping standard. When a certain Earth satellite “ S “ above the ground emits a signal at the time t1, the instantaneous position point in space where “ S “ is located is set as “ A “; When the GNSS receiver at ground station “ C “ receives the signal from “ S “ at time t2, the satellite has moved to the position of point “ B “ above the ground (as shown in Figure 5).

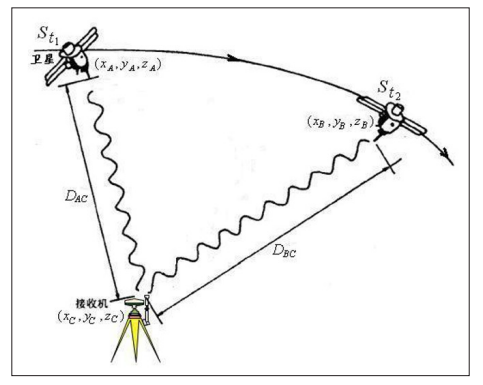
Figure 5: The actual spatial distance traveled by the satellite signal

Then, the current international consensus in the GNSS measurement process is to determine the distance between the satellite and the observation point C( xC,yC,zC ) is determined by using the 3-dimensional coordinate value ( xA,yA,zA ) at point A, as published in the satellite ephemeris received by the GNSS receiver, as the starting point for the spatial distance travelled by the satellite signal during this time. There is an inevitable problem here: if the satellite is free and stationary over the Earth at point A, then there is no dispute that the GNSS receiver at observation point C measures the satellite signal propagation distance in space as DAC. However, when the satellite is free to move to point A and instantaneously emits the signal, is the propagation distance of the satellite signal measured by the GNSS receiver at point C still DAC? This is uncertain, because this distance is derived from a 3-dimensional space with the Earth as a stationary system. If we look at it from the satellite’s point of view, then the actual propagation distance of the satellite signal in space measured by the GNSS receiver is not DAC, but the distance DBC between the point B( xB,yB,zB ), the spatial position to which the satellite is moving, and the point C, where the receiver is located, at the moment the receiver receives the satellite signal! Therefore, when we use A the coordinates of the point as the starting point of GNSS ranging, there is already a certain gross error in the direction of the 3 axes from the beginning! That is

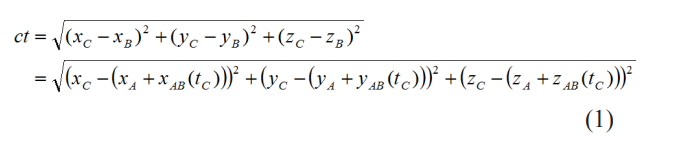
Of course, we now deal with this error in terms of Einstein’s relativity effect, that is, according to the special and general theory of relativity, the frequency shift of motion and gravitational frequency shift occurs when a clock of frequency f0 on the ground is placed on a satellite traveling at a certain speed vs, and the resulting total time error is assumed to be Δts, without taking into account the effects of the Earth’s rotation and other factors such as satellite ephemeris errors and signal propagation errors The spatial distance ( D=ct ) traveled by the satellite signal during the time ( t12=t2-t1 ) is usually the result of eliminating Δts, i.e [8-12].

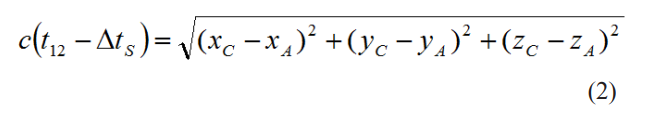
Obviously, the measurement results obtained from the two ways of handling errors mentioned above are actually different. The measurement errors Δxc,Δyc,Δzc, based on the principle of Equation (1) are correlated and independent variables, whereas the Δxc,Δyc,Δzc based on the principle of Equation (2) are uncorrelated and dependent variables. At the same time, according to the principle of Eq. (1), if we consider the coordinate value of the point as the starting point B to solve the coordinates of the observation point C, the measurement results obtained can also directly disregard the rotation of the Earth and the multi-body problem, which can naturally exclude the world-wide problem that there is no exact solution for the multi-body problem above three bodies [13-16].

Discussion

It can be judged that it is a misunderstanding that the results of Michelson’s interference experiment and Bradley’s discovery of optical aberration are in conflict. The spatial distance between the light source and the light receiver is essentially the distance between two points in a higher dimensional space of 4 dimensions or more, and this distance will change in time due to the relative motion between the light source and the light receiver. This distance undergoes a change in time due to the relative motion between the source and receiver points. In contrast, interference experiments are conducted between several relatively stationary points on an interferometer that moves with the Earth, all of which are in the same 3-dimensional space with the Earth as the frame of reference, and no matter how the Earth moves in the universe, the distance propagated between the light source and the receiving points always represents the distance between two points in a 3-dimensional space; under this premise, the distance between two points in a 3-dimensional space is always represented by the light. Even if the Earth rotates on its own and revolves around the Sun, any of the same distances (either parallel or perpendicular to the direction of the Earth’s motion) that the light travels on the interferometer will experience the same temporal variation.

By the same token it can also be understood that the mutual motion of the various stars in the universe, as well as the interaction between the various objects or particles, are not actually the result of the existence of a force of any kind, but rather they are each located in several different 3-dimensional spaces within the same higher dimensional space, respectively. Although, in the perspective accustomed to 3-dimensional space, it is commonly believed that they are in motion; but from the perspective of higher dimensional space, they themselves are all essentially stationary in the universe, and not really in motion! It is like several objects placed at rest at several location points on the surface of the earth, and we certainly do not think about whether there exists a force of any kind acting to maintain the relative rest state between them in the horizontal direction.

Conclusion

In short, the so-called “invariance of the speed of light” is not the result of “different distances for different times”, but the result of “the same distance for the same time”. In other words, the distance traveled and the time spent by light between any two free objects in space are the same for any frame of reference!

References

1. Einstein Albert (1961) Relativity the Special and the General Theory: A Popular Exposition. New York:
2. Einstein Albert (1988) The Meaning of Relativity Including the Relativistic Theory of the Non-Symmetric Field - Fifth Princeton: Princeton University Press.
3. Hawking Stephen (1988) A Brief History of Time From the Big Bang to Black Holes. New York: Bantam Books.
4. Thorne Kip (1994) Black Holes and Time New York: Norton.
5. Qien Li (1980) The study on the incompatibility between superluminal speed and relativity. Guangzhou: Journal of Jinan
6. Di Hua (2009) A fundamental revision of Einstein’s theory of relativity: relativistic mechanics with variable speed of light (Part I). Frontier
7. Di Hua (2010) A fundamental revision of Einstein’s theory of relativity: relativistic mechanics with variable speed of light (Part II). Frontier
8. Shaoquan Xu (2001) Principle and Application of GNSS Hubei: Wuhan University Press.
9. Xuesen Li, Lantao Wang, Shaoyuan Li (1998) Relativistic effects and their effects on GNSS Surveying and Mapping Science 1: 32-38.
10. Mengyang Zhang, Baowei Lv, Song Wenmiao Song (1998) The effect of relativistic effect on the accuracy of GNSS single point positioning. Journal of Electronics and Information 20: 663-668.
11. Neil Ashby (2002) Relativity and the global positioning system [J]. Physics Today 5:
12. Baojun Fei, Zhenghong Chen (2003) More study on the relativistic effect of Journal of Armored Forces Engineering College 17: 1-3.
13. Allen DW, Weiss MA, Ashby N (1985) Around-the-world Relativistic Sagnac Science 228: 69-70.
14. Min Yao, Shengyuan Zhu, Rongshi Pan (1988) Relativistic effects of artificial earth satellites in geocentric system. Journal of Astronomy 29: 181-189.
15. Hanwei Zhang, Yong Zheng, Lan Du (2003) Relativistic Delay Model for VLBI Observation of Artificial Earth Journal of Surveying and Mapping.
16. Ruyong Wang (2009) Extended Sagnac effect, GNSS and the experimental test of two principles of special relativity [J]. Journal of Beijing Institute of Petroleum and Chemical Technology 17: 53-57.