Author(s):
The present work calls attention to an undeclared assumption made by Einstein in his landmark paper [Ann. Physik 322 (10), 891 (1905)] in which he introduced the Special Theory of Relativity (STR). The emphasis in textbooks and periodi-cals is always on his two postulates of relativity [the Relativity Principle (RP) and the constancy of the speed of light in free space]. Yet, the well-known results of his theory such as Fitzgerald-Lorentz length contraction (FLC) and the symmetry of time dilation (two clocks in motion each running slower than the other) are based exclusively on this third postulate. It is shown that an alternative assumption of clock-rate proportionality (Newtonian Simultaneity) is also consistent with Einstein’s first two postulates and with the Relativistic Velocity Transformation (RVT), but that it leads to a fundamentally different space-time transformation than the Lorentz Transformation (LT) of STR. It is referred to as the Newton-Voigt Transformation (NVT). Its predictions regarding length and time measurements by moving observers differ sharply from those of the LT. A “clock riddle,” distinct from the well-known “clock paradox,” is presented to underscore the differences between these two versions of the relativistic space-time transformation. It is shown that the NVT is consistent with remote simultaneity and the impossibility of time inversion, and therefore does not rule out the existence of faster-than-c particles under the condition that they have null proper mass
The first relativistic space-time version was derived by Voigt in 1887 [1]. It differs by a common factor in all four equations from the version published in Einstein’s original paper on the Special Theory of Relativity (STR) known as the Lorentz transformation (LT) [2]. For example, the relation between the y and y’ spatial coordinates is given by Voigt as y’= (1-v2 c-2)0.5 y = λ-1y (c is the speed of light in free space defined to have a value of 299792481 s-1 and v is the relative speed of the two observers related in the transformation) rather than simply as y’=y prescribed in the LT [2, 3]. In the intervening time (1899), Lorentz had written down a more general form of the transformation in which he included a common undefined factor of ε on the righthand side of each equation [4, 5]. Einstein was aware of this degree of freedom in the general LT, referring to the “as yet unknown” factor as θ instead of Lorentz’s ε. He went a step further than Lorentz, however, and claimed on p. 900 that θ is a function of only a single variable, namely v, the relative speed of the two rest frames involved in the transformation [2]. It is noteworthy that Einstein does not even refer to the latter characteristic of θ as an assumption. He simply states it as a matter of fact and gives no justification whatsoever for this conclusion. He then goes on to show by symmetry arguments that the only possible value for θ (v) is unity, which in turn leads to the aforementioned y’=y relation in the LT. Although there have been countless derivations of the LT in textbooks and review articles over the years since Einstein’s original work, no one seems to have made a serious attempt to justify the above assumption, which amounts to a third postulate of STR, other than to state in broad terms that the resulting theory has been so successful in its predictions that there is no reason to doubt any aspect of it. The most common procedure is to define the LT in terms of various coefficients in the transformation and state without further discussion that they also can only depend on the relative speed v [6-8]. Other authors such as Goldstein deal with the matter by asserting that it is somehow inescapable that two observers must agree on the values of distances measured along a direction perpendicular to that of their relative velocity (y’=y, for example) [9].
In the present work, a more critical approach is taken with regard to Einstein’s undeclared assumption to see if another choice for the “normalization” function in the LT might perform just as well as the original in describing available experimental data. Among other things, the question will be raised as to what other variables might reasonably be assumed to have an influence on the value of θ in specific cases. To begin the discussion, an example will be considered in which the y’=y prediction of the LT is tested directly by employing the light-speed postulate without any further assumptions.
Einstein’s second postulate states that the speed of light in free space is independent of the states of motion of the source and the observer. One of the practical consequences of this postulate is that it allows distances to be measured by means of proper clocks of each observer. The modern-day definition of the meter is based on this possibility: it is the distance light travels in c-1 s [10].
Consider the following example that will be referred to in the following discussion as the “clock riddle” (to distinguish it from the oft-discussed “clock paradox”). Two observers O and O’ approach each other along the x, x’ axis of their respective coordinate systems with relative speed v. They wish to measure the distance between two fixed points in the rest frame of one of them (it doesn’t matter which) along a direction that is perpendicular to their relative velocity. Because of time dilation in the rest frame of O’, his proper clock is known to run λ times slower than those in the rest frame of O; thus, their respective clock readings satisfy the relationship, t’ = λ-1t, in all cases. The second postulate ensures that their respective values for the aforementioned distance can be obtained by multiplying the elapsed time on each clock with c. As a result, O finds that the distance is y=ct, whereas O’ finds that it is y’=ct’. Because of the above relationship between their respective measured times, this means that y’ = ct’ = λ-1ct = λ-1y. However, this result stands in contradiction to the Fitzgerald-Lorentz length contraction effect (FLC) that Einstein derived on the basis of the LT [2]. The FLC states on the contrary that y’=y because the direction is perpendicular to the relative speed of the two observers. Moreover, the same argument leads to a different result from the FLC when a distance is measured along the x, x’ axis that is parallel to their relative velocity. The ratio of their respective clock rates again completely determines the ratio of their measured lengths in any direction. Hence, x’= λ-1x in this case, i.e. the value measured by O’ is shorter than that obtained by O simply because of the aforementioned difference in the rates of their respective proper clocks. This result also stands in contradiction to the FLC, since it predicts that x’=λx, i.e. the observer (O’) with the slower clock measures a larger value for distances along any axis that runs parallel to their relative velocity [2]. The above example shows that different results are obtained from STR depending on how the theory is applied. This is the clock riddle. Either one has to find an error in one of the procedures employed to obtain the two sets of results, or one has to amend the theory in such a way as to remove the inconsistency in a logically transparent manner. The first of these arguments finds that, as a direct consequence of time dilation, O and O’ disagree on their respective measured values for the distance between the two points along the y, y’ axis. This conclusion rests squarely on Einstein’s light speed postulate. Since the LT also depends in an essential way on the same postulate, it is clear that eliminating it would be fatal for both approaches. Besides, there is ample experimental evidence in favor of the constancy of the speed of light in free space, so removing it from the list of underlying premises of relativity theory is really not a viable option. On the other hand, as already discussed in the Introduction, there is another assumption, Einstein’s “third postulate,” in the derivation of the LT that could be the cause of the problem. This state of affairs makes it all the more advisable to take a closer look at his conclusion that the normalization function θ can only depend on the relative speed v of the two observers. This is especially desirable when it is realized that the same assumption automatically forces the conclusion that the two observers must agree on any distance measured along a direction that is perpendicular to their relative velocity. In effect, Einstein has simply assumed that y’=y, not actually derived it on the basis of his main two postulates alone.
There is a fundamental principle for correcting physical theories when their assumptions are violated: amend the theory in such a way so as to bring it into agreement with the new experimental data while at the same time leaving its earlier successful predictions intact. This goal is easily achieved in the present case because of the relativistic velocity transition (RVT):
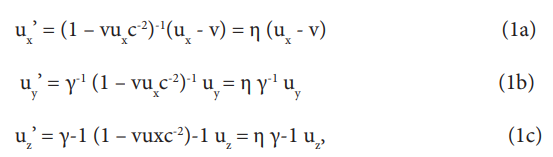
where u’ and u are the respective velocities of the object of the measurement for two observers moving along the common x, x’ axis with relative speed v, and n = (1– vuxc-2)-1. The RVT has many successful predictions/explanations to its credit: the Fresnel light drag experiment, the aberration of starlight at the zenith, Thomas spin precession, the Sagnac effect, and the general fact that the speed of light in free space is the same for all observers.
The key point in the present context is that the derivation of the RVT does not depend in any way on the choice of θ in the general version of the LT:


One simply has to obtain the desired RVT relationships in eqs. (1a-c) by dividing eqs. (2a-c) for x’, y’ and z’ by eq. (2d) for t’ in each instance, i.e. ux’ = x’/t’ etc. Indeed, the fact that θ is eliminated in all such velocity determinations is the underlying reason why such a normalization function cannot be defined on the basis of the second postulate alone (actually, there is an additional assumption required for this conclusion, namely that θ is constant; this point will be discussed subsequently). As a result, it is possible to obtain an alternative version of the Lorentz transformation (ALT) that is just as consistent with Einstein’s first two postulates as the original LT, but one which is internally consistent with the rest of the theory. The choice of θ is made on the basis of the experimental result for time dilation, namely that proper clocks in different rest frames always have strictly proportional rates (and not necessarily with the ratio claimed in STR): t’=t/Q [11]. To do this one has to eliminate Einstein’s unsubstantiated assumption for θ and replace it with a correct version whose value also depends on the speed of the object of the measurement for each observer, not just their speed v relative to one another. Alternatively, one can start with the RVT in eqs. (1a-c) and simply multiply it with the above proportionality relationship for measured times.

One can obtain the original LT in an analogous manner by multiplying the RVT with t’ = λn-1 t. The latter corresponds to Einstein’s value of θ = 1 in eq. (2d) of the general LT, whereas θ=n (λQ) -1 in the ALT, as is evident from its equations for y’ and z’. As remarked above, it is necessary to remove the assumption that θ is a constant to have a sufficiently general derivation in both cases. This can be done by assuming that the RVT is valid on an instantaneous basis, i.e. even when the relative speed v is not constant at the time of measurement. The derivations can then proceed as before by using intervals in the definitions of the velocity components, i.e. ux’ = δx’/δt’ etc., thereby leading to intervalal forms for both the LT and the ALT. This procedure also leaves open the possibility that the proportionality factor Q in these equations is time-dependent [12, 13]. Altering the value of θ removes the above contradiction with Einstein’s second postulate, but this change only affects earlier predictions of STR that have never received experimental confirmation. For example, the relationship between the energy and momentum of accelerated particles in the laboratory is unaffected by this change in relativity theory because it only alters predictions involving space and time. At the same time, the ALT removes the subjective character of the theory that is based on the LT. It is always possible to say which clock is slower and by what ratio in the revised theory; one simply has to know the value of the proportionality constant Q in the above formula. The resulting objective theory also has consequences for the measurements of all other physical variables for moving observers. For this reason, the ALT might more appropriately be called the OLT, the objective version of the Lorentz transformation. More details concerning this revised version of relativity theory may be found in earlier publications [12, 13].
Perhaps the most significant characteristic of the ALT is that it no longer insists upon the mixing of space and time in its formulation. What has apparently not been recognized over the many years of experience with the LT is that the lightspeed and relativity postulates can be equally well satisfied by assuming that there is always a strict proportionality between clock rates of different observers independent of their position in space. When measured time intervals are compared for two observers in relative motion, different results occur depending on the value of θ in eq. (2d). If, as assumed for the LT,

As a result, two events that occur simultaneously for one observer (δt = 0) will not be simultaneous for the other as long as δx = 0, i.e. the events occur at different locations and v≠ 0. It is critical to compare the above prediction of “remote non-simultaneity” with the effect of proportional time dilation also derived from the LT. On the one hand, the theory claims that two time differences δt and δt’ for the same event, such as a pair of lightning strikes in a forest, satsify a proportionality relation, i.e. δt= Xδt’. Yet, at the same time, the theory claims that one of the time differences can be exactly zero (simultaneous observation in a given rest frame), i.e. δt’=0, whereas the other is different from zero, i.e. δt≠0, because the strikes occur at different times for the other. This is impossible since such a conclusion requires that one deny the axiom of algebra which demands that multiplication of zero by any number, in this case the time-dilation proportionality factor X, must result in a product of zero as well. Since both predictions stem from the LT, it is clear that this space-time transformation is physically untenable, and therefore cannot serve as a valid component of the true relativity theory. The above argument has been referred to as the “Clock Puzzle” in previous work, to distinguish it from both the Clock Paradox and the Clock Riddle mentioned in Sect. II [14]. Moreover, it also needs to be recognized the LT leaves open the possibility that two events can occur in a different order if vc-2 (δx/ δt)>1 in eq. (4). The latter condition can theoretically occur if the speed of an object, δx/δt, is greater than c. Neither of the above time relationships is consistent with the ALT, however. According to eq. (3d), the analogous relation to eq. (4) is simply:

Clearly, one of the time intervals can never be zero without the other one also being zero (remote simultaneity). Furthermore, since the proportionality constant Q is always positive according to experience with time dilation, it follows from eq. (5) that δt’ and δt must always have the same sign [11]. Hence the time-reversal phenomenon is also not possible according to the ALT. Recent experiments at CERN have brought new interest into this general area by indicating strongly that neutrinos can move at faster-than-c speeds. The belief that the speed of photons can exceed c has a long history, dating back to Wien’s discussion of the consequences of light passing through a region of anomalous dispersion. Since the refractive index n can be less than unity under these circumstances, it was argued that both the phase (c/n) and group velocities (c/ng ) might exceed c in such regions. Sommerfeld and Brillouin presented arguments in 1907 to show that anomalous dispersion could be reconciled with STR as long as the corresponding “signal” and energy velocities do not exceed c [15, 16 & 2]. Nonetheless, in more recent times, experimental evidence has been presented which shows clearly that single photons do propagate with u>c speeds in the neighborhood of absorption lines [17, 18]. Also in this case, however, there has been a general reluctance to accept this result at face value, again because it is thought to be inconsistent with STR and the LT [18, 19]. The ALT, on the other hand, is basically non-committal about faster-than-c flight for a particle. There is certainly no reason to reject the idea outright on this basis, especially since, as already mentioned, time reversal itself is ruled out because of eq. (5). The RVT of eqs. (1a-c) predicts that, assuming the relative speed v of the observers is less than c, either both of them will find the speed of an object to be u<c, or in the present case of interest, both of them will find the object to moving with u>c [20, 21]. The intermediate situation, of course, has them agreeing that the speed of the object is exactly u=c, in agreement with.
Einstein’s second postulate. In short, if it were not for the strict belief in the LT, physicists would have no valid reason to reject faster-than-c flight other than a failure of experiment to provide confirmed positive evidence for the phenomenon. Before closing this discussion, it is important to add that one of the standard objections to faster-than-c flight has nothing to do with the LT. Einstein pointed out in his original work that particles with non-zero proper mass would experience a singularity in their kinetic energy when accelerated to u=c, and he thus argued that speeds at or above this level are forbidden to such entities, e.g. electrons [1]. However, that position leaves open the possibility that photons are exempt from this restriction by virtue of their null proper mass, and this conclusion has been generally accepted by the physics community over the succeeding century. As a consequence, it seems that there is a simple way out of the current dilemma with neutrinos, namely to assume that they also have exactly null proper mass, and thus are no more restricted to a minimal speed than are photons in anomalously dispersive media. Whether there is a comparable medium that would lead to the acceleration of neutrinos can certainly be questioned, however, in view of their nearly complete inability to interact with other forms of matter [22].
The second postulate of STR is incompatible with the y’=y equation in the LT. It is logically inconsistent to claim that two observers who agree on the value of the speed of light will also agree on the distance travelled by the light when their respective proper clocks run at different rates (“Clock Riddle”). The y’=y condition is not an inevitable consequence of the light speed postulate, but rather is caused by an undeclared, third postulate/assumption in Einstein’s original paper regarding the supposed dependence of a normalization function appearing in the general form of the LT. The inconsistency is removed by assuming instead that proper clocks in relative motion always run at strictly proportional rates (t’=t/Q), consistent with all experimental data as yet obtained demonstrating time dilation. This leads to a different form for the above normalization function and an alternative form of the LT that is perfectly consistent with Einstein’s first two postulates. The resulting ALT differs from its STR counterpart in a number of significant ways. First, it eliminates the symmetry condition that claims that two clocks in relative motion must both be running slower than each other. Secondly, it replaces the Fitzgerald-Lorentz length contraction effect with a version that is consistent with both the proportionality of clock rates and the second postulate. Accordingly, lengths expand isotropically in direct proportion to the rates of clocks in a given rest frame. The revised theory of length variations is consistent with an objective interpretation of the measurement process on a completely general basis. Thirdly, the ALT rejects the claim of remote non-simultaneity that has characterized STR since its inception. Since clock rates are strictly proportional to one another, it follows that two events that are simultaneous (δt’=0) for one observer must necessarily be simultaneous (δt=0) for any other observer (“Clock Puzzle”). Previous arguments that claim to have proven that events cannot be simultaneous for two observers in relative motion inevitably confuse the time of arrival of the news to the observers with the time of the actual occurrence of these events. Finally, the ALT removes the requirement of the LT that time reversal inevitably accompanies faster-than-c flight of particles. The usual reaction from proponents of STR when they are confronted with an inconsistency in their theory (including the recent findings of neutrinos traveling with faster-than-c speed) is to defend it by saying that it works so well in other applications that it can’t possibly have any deficiencies [23].
This attitude is patently false and is in direct conflict with the accepted principle for amending physical theories in general. It overlooks the possibility that a competing, “covering” theory can achieve the same successes as STR while at the same time avoiding the various contradictions that result because of Einstein’s undeclared assumption about the normalization function in deriving the LT. At the same time, it is imperative for any such covering theory to prove that it is capable of explaining all available experimental data in a clear and concise manner without introducing new untenable assumptions into the underlying postulatory structure. By maintaining consistency with Einstein’s RVT, the ALT succeeds in achieving this goal without exception for experiments involving measurements of space and time, while leaving untouched those successful predictions of STR that involve other variables such as energy and momentum.
