Author(s): <p>V.G. Plekhanov</p>
Present paper is devoted to the non - accelerator manifestation of the strong nuclear interaction - the heart of quantum chromodynamics (QCD) which is part of the Standard Model (SM). The observation of isotopic shift (0.103 eV) of the zero - phonon emission line in photoluminescence spectra of LiD crystals (possessing a strict interaction in the deuterium nucleus) comparison with LiH (in the hydrogen nucleus of which there is no strong interaction) is a first direct proof of the strong nuclear long - range character. The non - accelerating measurement of the strong interaction constant from the distance between nucleons made it possible to find the maximum possible value of αs = 2.4680. The isotopic acquisition of mass by massless fermions is briefly discussed
Modern physics distinguishes three fundamental properties of atomic nuclei: mass, spin (and related magnetic moment), volume (surrounding field strength), which are the source of isotope effect [1]. Particles Physics grew from nuclear physics. Elementary particles are the most fundamental building block of matter. Elementary particles of our own time are quarks together with leptons such as electron. Unlike nuclear physics, particle physics does have a comprehensive theory but altogether the Standard Model (SM) is very successful at explaining a wide range of phenomena, there are still questions that remain to be answered [2, 3]. One of such question is the a nature strong nuclear interaction. A common place in modern physics is the short - range of strong nuclear interaction - the heart of quantum chromodynamics (QCD), which is part of SM. Great advances in particle physics have been attained in the last several decades. All these results were concentrated into simple and beautiful theory, known as the SM in the late 1960’s which formulated in the framework of non - Abelian gauge theory and was extremely successful in describing a wide range of existing phenomena of elementary particles. The SM embodies our knowledge of the strong and electroweak interactions. It requires as input 19 independent parameters. These are three charged lepton masses, six quark masses, three gauge coupling constants, three quark mixing angles and one complex phase, a Higgs mass and quartic coupling constants, and QCD vacuum angle. In the SM, the structure of nucleons is specified in terms of quarks and gluons, but unanswered questions remain [2, 3]. One concerns the spin of the proton and other - with proton radius puzzle. The SM asserts that the material in the Universe is made up of elementary fermions interacting through fields, of which they are the sources. The particles associated with the interaction fields are bosons [5]. The lack of experimental proof for this strong statement is tacitly perceived as only corect. This paper is the first attempt, by invesigating the remarkable properties of the mass isotope effect, to illuminate the origin of the strong nuclear interaction. The non - accelerator observation of isotopic shift (0.103 eV) of the zero - phonon emission line in photoluminescence spectrum of LiD crystals (possessing a strict interaction in the deuterium nucleus) is a direct proof of the stong nuclear long - range character.
A brief history of this issue connecting with the nature of the strong nuclear interaction is as follows. As we all know in 1932 the neutron (n) was discovered and the modern atomic structure was complete with massive nucleus consisting of protons (p) and neutrons surrounded by a "cloud" of light electrons [4, 5]. The discovery of the neutron by Chadwick in 1932 may be viewed as the birth of the strong nuclear interaction: it indicated that nucleus consists of protons and neutrons and hence the presence of force that holds them together strong enough to counteract the electromagnetic repulsion [4]. In 1935 Yukawa have tried to develop a theory of nuclear forces [6]. Yutaka’s potential has the form
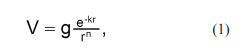
for some n. Here the strength of the force is measured by the constant k [5]. The most important feature Yukawa’s forces is that they have a small range (~ 10-15 m). The central dogma of atomic physics after Yukawa’s paper that proton - electron attraction could be explained in terms of classical electrostatic theory, while the strong force effects were essentially new and inexplicable. So, far the best theoretical guess is the Yutaka potential, but it is a static potential not dependent on velocities of the nucleons. A static force is not a complete one because it can not explain the propagation of the nuclear interaction. Moreover, as was indicated above, a phenomenological Yutaka potential can not be directly verified experimentally. We should note that nowadays in text books and elsewhere the separation of electromagnetic and strong interaction tacitly assumed. It is very strange up to present time we do not even know the strong force very well. And what is more we have some contradiction taking into account that the forces between quarks must be long - range, because the gluons have zero mass. But as was mentioned above the force between colorless hadrons is short - range, when the distance between hadrons is more than nuclear size [7]. We can see that the border of the nuclear size transforms long - range interaction in the short - range one. It is very old qustion which up to present time has not any theoretical explanation.
Obviously we should remember that all structure nucleus and nucleons are a successful experiments in scattering different particles. However performing scattering experiments would not be enough to study the laws of subatomic physics [6]. Therefore discovering new methods, besides scattering, would be beneficial for such study. Recently we have shown that the origin of the isotope is due the strong nuclear interaction in solids and presented it in a series of international conferences on high energy physics [7]. The present paper devoted to to description of the remarkable propertis of the isotope effect.
Modern physics distinguishes three fundamental properties of atomic nuclei: mass, spin (and related magnetic moment), volume (surrounding field strength), which are the source of isotope effect. The stable elementary particles (electrons, protons and neutrons) have intrinsic properties. Isotopically pure materials represent a separate class of modern materials science, which is an accelerator of the development of the latest fine technology. First of all, it is necessary to remember due to this explosive leap in the development of electronic and optical technologies. It is thanks to isotopically pure silicon used in personal computer processors that it has been possible to step beyond the 3GHz threshold. Moreover, isotopically pure germanium is the best weak signal detector. Low dimensional structures of quantum wires (QW), quantum dots (QD) received a new impetus for development when using isotopically pure materials, as well as artificially regulating the isotopic composition of a material.
The experimental results presented in this work were obtained by the methods of standard classical spectroscopy and were described in detail earlier (see, for instance, reviews [8, 9]. The isotope effect has the following remarkable properties:
1. Isotopic creation of new materials;
2. The isotopically generated maximum possible value of strong coupling constant αs;
3. Isotopic acquisition of matter.
The first substane is LiH, which has the maximum value of the mass isotopic effect. When hydrogen is replaced by deuterium a new substance (lithium deuteride) is obtained, which as will be shown below, using the example of electronic and phonon excitations has new characteristics that differ from previous ones.
Photoluminescence is the optical radiation emitted by a physical system (in excess of the thermal equilibrium blackbody radiation) resulting from excitation to a nonequilibrium state by irradiation with light. Photoluminescence is also rapidly evolving into major basic research tool comparable to absorption (reflection) measurements in importance. Two reason for this stand out as significant. First is the sensitivity of the luminescence technique. It often happens that features which are just discernible in absorption will completely dominate the luminescence spectra. The converse is also sometimes true, making luminescence and absorption (reflection) complementary techniques. Second is the simplicity of data collection. In last half- century the luminescence method has become one of the most common techniques for studying excitons in dielectrics and semiconductors. While the structure of spectra of fundamental reflection (absorption) depends on the internal degrees of freedom of Wannier - Mott exciton, the structure and shape of the luminescence spectrum are determined primarily by its external degrees of freedom [10]. The latter are associated with the translation motion of large - radius exciton as a whole, with the translation mass M = me + mh [1], where me and mh - effective masses of electron and hole, respectively
As was shon earlier, free exciton luminescence is observed when LiH (LiD) crystals are excited in the midst of the fundamental absorption [1, 9]. The spectrum of free exciton photoluminescence of LiH crystals cleaved in superfluid helium consists of a narrow (in the best crystals, its half - width is ?E ≤ 10 meV) phononless emission line and its broader phonon repetitions, which arise due to radiated annihilation of excitons with the production of one to five longitudinal optical (LO) phonons (see Fig. 1).
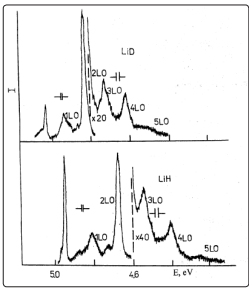
Figure 1: Photoluminescence spectra of free excitons at 2 K in LiH and LiD crystals cleaved in superfluid helium
The phononless emission line coincides in an almost resonant way with the reflection line of the exciton ground state which is indication of the direct electron transition X1 - X4 of the first Brillouin zone [11]. The lines of phonon replicas form an equidistant series biased toward lower energies from the resonance emission line of excitons. The energy difference between these lines in LiH crystals is about 140 meV, which is very close to the calculated energy of the LO phonon in the middle of the Brillouin zone [12]. As we can see from Fig. 1 the photoluminescence spectrum of LiD crystals is largely similar to the spectrum of intrinsic luminescence of LiH crystals. There are, however, some distinctions one is related. Firstly the zero - phonon emission line of free excitons in LiD crystals shifts to the short - wavelength side on 103 meV. These results directly show the violation of the strong conclusion (see, e.g. [2, 3, 5] and references quoted therein) that the strong force does not act on leptons. The second difference concludes in less value of the LO phonon energy, which is equal to 104 meV. The simplest approximation, in which crystals of mixed isotopic composition are treated as crystals of identical atoms having the average isotopic mass, is referred to as virtual crystal approximation (VCA) [1].
The measurements of the low temperature of reflection and luminescence spectra of the whole series of mixed crystals LiHx D1-x is permitted to obtain the dependence of the interband transition energy on the isotopes concentration [9]. Taking into account that the concentration is to vary directly the lattice constant we are plotting the dependence of the band - gap energy (the power of the force strong interaction) on the distance between nucleons depicted (Fig 2) [1].

Figure 2: The force dependence of strong nuclear interaction on the distance between nucleons in deuterium nucleus. The straight dashed line is the linear dependence of the force force dependnce in the virtual model.
The next isotopic creation material is diamond. We emphasize that due to the wide class of allotropic carbon compounds, the physical properties of which vary from transparent in the ultraviolet (UV) range (diamond) to opaque (graphite, graphene), from dielectric (diamond) to a compound with metallic conductivity (graphene) and also which have extremely different elastic and thermal properties - all of the above mentioned characteristics exhibit isotopic dependence. We must substitute 12C for a heavy isotope 13C. Carbon atom is built from 6 protons, A neutrons and 6 electrons, where A = 6 or 7, yield the stable isotopes 12C and 13C, respectively, and A = 8 characterizes the radioactive isotope 14C [5, 13]. The isotope 12C, with nuclear spin I = 0, is the most common one in nature with 99% of all carbon atoms, whereas only = 1% are 13C with nuclear spin I = 1/2. There only traces of 14C (10-12 of all carbon atoms) which transforms into nitrogen 14N by β - decays. Although 14C only occurs rarely, it is important isotope used for historical dating [14]. Carbon, one of the most elements in nature, still gives a lot surprises. It is found in many different forms - allotropes - from zero dimensional fullerene, one dimensional carbon nanotubes, two dimensional graphene and graphite, to three dimensional diamond - and the properties of the various carbon allotropes can vary widely [7]. For instance, diamond is the hardest material, while graphite is one of the softest; diamond is transparent to the visible part of spectrum, while graphite is opaque; diamond is an electrical insulator, while graphite and graphene are a conductors. Very important is that all these different properties originate from the same carbon atoms, simply with different arrangements of the atomic structure. Below we describe the new phenomena of the carbon - isotope effect in diamond. Crystals 12C and 13C diamond differ only one neutron.
Due to the indirect gap of Eg = 5.47 ± 0.005 eV (295 K), at K = 0.76 X, diamond has intrinsic phonon - assisted free exciton luminescence lines [8, 9]. The change of the indirect gap of diamond between pure 12C and 13C crystals has been numerous determined (see, e.g. and reference quoted therein) [7]. Fig. 3 presented the results of paper [14]. We can see the continuous increase the band - gap with growth of the 13C concentration. This is a direct show the act of the strong interaction on the leptons [3]. Watanabe et all. Have concluded that the maximum change of the band gap due to substitution of 12C by 13C is ?Eg = 15.4 meV. This value per one neutron and on seven neutrons we get 15.4 x 7 =108 meV. This value is very close to the observed one (103 meV) in LiD crystals.

Figure 3: Luminescence spectra of free excitons in homoepitaxial diamond films grown from mixture of methane in hydrogen by means of a microwave plasma - assisted CVD. The spectra illustrate the effects of isotope composition 12C1-x 13 Cx ( x 0.001; 0.247; 0.494; 0.740; and 0.987) mixed in the CVD gas phase. All spectra are normalized to the same height (after [14]).
Raman spectroscopy is a powerful means to gain experimental access to phonons and their interaction and scattering mechanisms [8, 9]. First - order Raman light scattering spectrum in diamond crystals also includes one line with maximum ωLTO(γ) = 1332.5 cm-1 [14]. In Fig. 4 the first - order scattering spectrum in diamond crystals with different isotope concentrations is shown [7]. As was shown in, the maximum and width of the first - order scattering line in isotopically - mixed diamond crystals are nonlinearly dependent on the concentration of isotopes x [9]. The maximum shift of this line is 52.3 cm-1, corresponding to the two limiting values of x = 0 and x = 1. The effect of the isotopic 12C to 13C ratio on the first - and second - order Raman scattering of light in the diamond has been numerous investigated. As 13C content is increased from the natural ratio (12C/13C = (1 - x)/x, where x = 0.011 to the almost pure 13C (x = 0.987) the whole spectrum has shifted towards longer wavelength (Fig. 4) in good agreement with the expected M-0.5 frequency dependence on the reduced mass M. For an approximately equal mix of the two isotopes, the authors reported that the feature seen in the above two - phonon spectra were either broadened or unresolved.
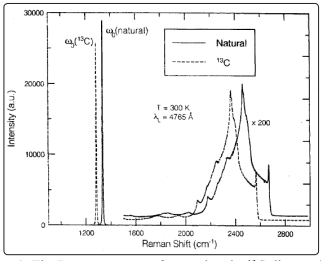
Figure 4: The Raman spectra of natural and a 13C diamond. The spectra show the dominant first - order Raman - active F2g line and the significantly weaker quasi - continuous multiphonon features (after [15]).
Traditionally nuclear - electron interaction (in our case neutron - electron interaction) taking into account the solving Schr?dinger equation using Born - Oppenheimer (adiabatic) approximation [16]. Since electrons are much faster and lighter than the nuclei by a factor nearly 2000 the electron charge can quickly rearrange itself in response to the slower motion of the nuclei, and this is the essence of the Born - Oppenheiemer approximations. This approximation results the omission of certain small terms which result from the transformation. As was shown in the eigenvalue (energy) of the electronic Schrö dinger equation (equation 6 in [17]) depends on the nuclear charges through the Coulomb potential, but doesn’t include any references to nuclear mass and it is the for the different isotopes. Besides this approximation, it is necessary to take into account a small contributions to isotopic shift through.

different for the hydrogen and deuterium nucleus. In this case the contribution equals 6 meV. Contributions to isotope shift of the zero - phonon emission line in luminescence spectra of LiD crystals as well as Lamb shift and specific Coulomb potential approximately equal 1, and 1 meV, respectively. These estimations are forcing us to search for new models and mechanisms of neutron - electron interaction including the results of subatomic physics, e.g. hadron - lepton interaction. By the way we should remind that during 20 century the problem of neutron - electron interaction was numerous investigation (see, e.g. [18, 19]). In these papers was shown the dependence of the electron energy level on the strong interaction, however, all the scientific literature on subatomic physics states that the strong interaction do not affects leptons (electrons etc.).
For the interpretation of our non - accelerator experimental results we should take into account the long range magnetic interaction which is a part of the electromagnetic field. Ordinary magnetic interaction of matter are determined by atomic magnetism [20]. Originally the hyperfine structure was taken to include those atomic effects (much smaller than the fine structure) that arise from the coupling between the electronic and nuclear angular moments. It is thus an internal effect in atoms, and we cannot switch it off or modify it except by changing the nuclear or electronic structure (going to excited states, for instance). The motion of the electrons produces a magnetic field Be at the nucleus, which interacts with the nuclear magnetic moment μN :

Typical energy differences of hyperfine multiplets are only about 10-7 eV (in case of the deuteron it is 3.16 10-7 eV). This value is by more than seven order less than we observe in experiments: the isotopic shift of the n 1s in LiD excitons is equal to 0.103 eV.
In view of such a discrepancy with the experimental value, it is perhaps reasonably to consider the possibility of some kind of manifestation of residual strong forces via anomalous magnetic moment of neutron, for example. How can the departure of the magnetic moments of the proton and the neutron from the "Dirac values" be understood. Before quarks were introduced, the explanation of the anomalous magnetic moments of the nucleons was based on virtual mesons that are present in their structures [5]. At the present time it is clear that nucleons are composed primarily of three quarks, the proton has the composition (uud), the neutron (udd) [2, 3]. Nucleons contain not just one point particle and a meson cloud; three point particles reside there. The interaction among the quarks, as we all know, is transmitted by gluons; the force is weak at short distances (4 0.1 fm) and strong at large ones (4 0.5 fm). The anomalous magnetic moments of the nucleons are due to hadronic effects, thus they cannot be computed to anywhere near the accuracy of the anomalous g factors for the leptons [2, 5].
Continuing the analysis of non - accelerator experimental observations, taking into account the theoretical works of Condon and Foldy we came to the unambiguous conclusion that the strong interaction affects the electronic excitations [18, 19]. Moreover, this fact indicates the long - range nature of the strong nuclear interaction. It is possible that this is a reflection of the long - range action of pions and gluons, especially in the infrared limit [20, 21]. Returning to Fig. 15 (in Ref. [22]), we point out that measuring the optical characteristics (reflection and luminescence) of a number of mixed crystals LiHx D1-x made it possible to plot the dependence of the forth (energy) of strong interaction of a distance between nucleons in the deuterium nucleus (Fig. 2) [22]. The results presented are the first measurements in the world scientific literature. Let us add that, as can be seen from Fig. 2 the observed dependence of the strong interaction force on the distance between nucleons is a nonlinear function. The experimentally observed increase in the value of the strong interaction energy in the region r ≥ 2 fm (rD = 2.1314 fm) agrees with qualitative picture in Fig. 6 of paragraph 2 [23, 22]. Using the magnitude of the anomalous value of the magnetic moment of the neutron and the experimentally observed value of the isotopic shift energy at 0.103 eV, the value of the strong interaction constant was found in the paper equal to 2.4680 which is very different from the results found from the data of accelerator technology (αs(Mz ) = 0.1198 ± 0.002 [24, 20]. It is well known that the coupling strength as αs is the basic free parameter of QCD, they of the strong interaction which is one of the four fundamental forces of nature. Confinement implies that the coupling strength αs, the analogue to the fine structure constant in QED, becomes large in the regime of large distance or low - momentum transfer interactions. (By the way in the world of quantum physics, "large" distances ?s correspond to 1 fm) 1 fm, "low" momentum transfers to Q (1 GeV/c) [2, 3]. Conversely, quarks and gluons are probed to behave like free particles, for short time intervals ("short" time intervals correspond to ?t ( 10-24 s.), in high - energy or short - distance reactions; they are said to be "asymptotically free", i.e. αs → 0 for momentum transfers Q → ∞ [2, 3, 5, 25]. The value as, at a given energy or momentum transfer scale Q, must be obtained from experiment. Determining αs at a specific energy scale q is therefore a fundamental measurement, to be compared with measurement of the electromagnetic coupling α. Taking into account that in our experiments we study strong force on very large distance (≈ 104 more than in nuclear physics) we may expect the very large value of αs (compare to the results of Fig. 6 Ref.) [25]. Moreover, our experimental results allow to determine αs in rather large energy scale (see Fig. 2). Thus, for the first time in a non - accelerator experiments, the maximum value of the strong nuclear interaction coupling αs was obtained.
The remarkable properties of the graphene promise unheard of applications, especially in the semiconductor state. Especially graphene nanostructures are promising candidates for future nanoelectronics and solid - state quantum information technology. As was shown numerously, in the vicinity of K - points, the low - energy electron/hole dispersion relation is proportional to momentum, rather than its square (see, e.g. [7, 26]). This is analogous to the energy dispersion relation of massless relativistic electrons, so the electrons/ holes of graphene are described as Dirac fermions having no mass. In a simple neighbor model graphene is a semimetal with zero - overlap between valence and conduction bands. In order to make graphene a real technology, a special issue must be solved: creating an energy gap at K - points in the Brillouin zone (see, Fig. 5).

Figure 5: The energy dispersion of semimetal (solid line) and semiconductor (dashed line).
Different attempts have been made by researches, such as patterning graphene into nanoribbon, forming graphene quantum dots, making use of multilayer graphene sheet and applying an external electric field [7]. It was shown that the uniaxial strain can open a band gap in a metallic carbon nanotubes as well as carbon nanoribbon . As an example Fig. 6 shows the dependence of the energy of interband transition on the width of the graphene nanoribbons. The observed dependence is well described by the following expression Eg = α*/ (W - W*), where α* = 0.38 eV/ nm, and W* = 16 nm accounts for inactive edges [27].
This formula gives value of Eg equal to several eV, if W is reduced to a size, for example, 13C, but it is impossible. the isotopic transformation of graphene, a semimetal into emiconductor deserves special attention [28]. This means of the cones dispersion pattern E(k) at the K point of the Brillouin zone of graphene reformes into the usual parabolic dispersion of band structure pattern (see Fig. 5).
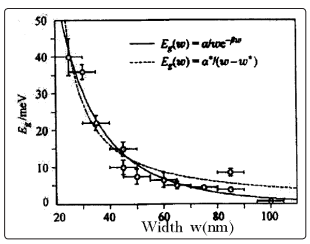
Figure 6: The dependence of Eg as a function of width of the graphene nanoribbons (after [27]).
According to the results of Ref. 22 this method can be used to obtain Eg of several hundred meV. since value of Eg depends on the concentration of 13C in graphene, this mechanism is easily realized either chemically or technologically. With the opening Eg of massless fermions (leptons = electrons) acquire mass. estimates of different ways of opening Eg in graphene give the following equality: Eg = 2m [28]. When Eg = 1 eV leptons acquire a mass equal 0.5 eV - the value is not large, but finite [22]. One of the mechanisms of acquire mass in elementary particle physics is considered in the paper [29]. This paper predicts that both quarks and gluons acquire running mass distribution in QCD, which are large at infrared momenta. The current quark of perturbative QCD evolves into a constituent quark as its momentum becomes smaller. The constituent quark mass arises from a cloud of low - momentum gluons attaching thenselves to the current quark. This is DCSB: an essentially nonperturbative effect that generates a quark mass from nothing; mamely it occurs even in the chiral limit. DCSB namely the generation of mass from nothing is a theoretically established nonperturbative feature of QCD. The solution of a gap equation shows that gluons are cannibals: they are paricle species whose members become massive by eating each other [20, 21, 29].
The isotope effect is a macroscopic manifestation of a strong nuclear force. The results of this work are the first attempt to unravel the nature of the short - range action of the Yukawa potential.
Many thanks to G.A. Plehhanov for improving my English.
