Author(s): Chiwa Musa Dalah*, Umar Yusuf Madaki and Ahmad Audu Daya
Malaria is a parasitic disease transmitted by female anopheles’ mosquitoes. It is a major cause of death in many developing countries of the world; also consider as one of the most prevalent diseases in tropical and subtropical areas. World Health Organization (WHO) estimated 216 million cases of malaria, 81% in the African region and there were 655,000 malaria deaths, 91% in the African region, and 86% were children under 5 years of age. Malaria is the third leading cause of death for children under five years worldwide, after pneumonia and diarrheal disease [1, 3]. The intensity of transmission depends on factors related to the parasite, the vector, the human host, and the environment.
Malaria is a parasitic disease transmitted by female anopheles’ mosquitoes. It is a major cause of death in many developing countries of the world; also consider as one of the most prevalent diseases in tropical and subtropical areas. World Health Organization (WHO) estimated 216 million cases of malaria, 81% in the African region and there were 655,000 malaria deaths, 91% in the African region, and 86% were children under 5 years of age. Malaria is the third leading cause of death for children under five years worldwide, after pneumonia and diarrheal disease [1, 3]. The intensity of transmission depends on factors related to the parasite, the vector, the human host, and the environment.
Transmission is more intense in places where the mosquito lifespan is longer (so that the parasite has time to complete its development inside the mosquito) and where it prefers to bite humans rather than other animals. Transmission also depends on climatic conditions that may affect the number and survival of mosquitoes, such as rainfall patterns, temperature and humidity [4]. The incidence of malaria has been growing recently due to increasing parasite drug-resistance and mosquito insecticide-resistance. Therefore, it is important to understand the important parameters in the transmission of the disease and develop effective solution and strategies for its prevention and control [2].
Many epidemic models have been analyzed mathematically and applied to specific diseases [3, 5]. Since the first mathematical model of malaria transmission is introduced by Ross [6], quite a few mathematical models have been formulated to investigate the transmission dynamics of malaria [6-13]. Ngwa and Shu [7] analyze a deterministic differential equation model for endemic malaria involving variable human and mosquito populations. We present an ordinary differential equation mathematical model for the spread of malaria in human and mosquito populations. Susceptible humans can be infected when they are bitten by an infectious mosquito. They then progress through the exposed, infectious, and recovered classes, before reentering the susceptible class. Susceptible mosquitoes can become infected when they bite infectious or recovered humans, and once infected they move through the exposed and infectious classes. Both species follow a logistic population model, with humans having immigration and disease-induced death.
In Nigeria, malaria prevalence is as high as 80 to 85% and is the most common cause of outpatient visits to health facilities. The malaria situation in Nigeria is very burdensome and it impedes human development. The degree of malaria infestation varies from region to region in Nigeria. The rate of malaria infection across space depends on dynamic processes involving complex climatic, environmental, physical, and social variables operating differently in space. This complexity makes the analysis of the spatial pattern of malaria infection in Nigeria important [2]. Yobe State is among the Nigerian States suffering from the scourge of malaria all year round.
In this work, the Researchers aimed to study the spread of malaria disease in Yobe State using a nonlinear dynamical system to qualitatively analyze its dynamics. Ross-Macdonald malaria model with mobile human hosts, mobile vectors and heterogeneous environment is considered.
Non Linear Dynamical Systems for Malaria transmission and control: Ross-Mac Donald model ?the spread of Malaria through Vector insect using RossMacDonald Model to enable make a prediction or determine the rate at which the disease is spreading.
For the fact that Ross-MacDonald Model depict the relationship between parameters and their changes with respect to time hence the need to answer these questions.
• Are there possible outbreak infecting the host community, Damaturu Local Government?
• What is the effect of vaccination in the given community prior to the arrival of diseases?
• What are the epidemic levels?
• How many will get infected if the epidemic takes off?
To determine the rate at which a Vector insect disease (Malaria) Spread with time and be able to project it impact over a short period of time
The emergence and re-emergence of Malaria Vector insect disease in the temperate state of this country that causes death to millions of children especially those below five (5) years of age is main point of concerned. Hence the need for this research. Significant of the study
A Ross-MacDonald Model is a model that predicts the exponential growth rate of malaria in a community of host Damaturu Local Government if no isolation was made especially in a closed population
A Stability Analysis method of solving Ross-MacDonald Model equation is employed completely so that the result obtained could be used as a tool for solving the problem
This research is mainly the Ross-MacDonald Model equation with much emphasis on the nonlinear system of Stability Analysis
To study the transmission and spread of malaria in two interacting population of humans (the host) and mosquitoes’ H (the vector), we formulate a model which subdivides the total human population size at time (t), denoted by S into susceptible humans exposed humans and recovered humans R0(t). Hence, we have; Let X(t) denote the numbers of infected humans and Y(t) Proportion of susceptible infections recovered at time t, respectively. Let a be the rate of biting on humans by a single mosquito (number of bites per unit time). Then the number of bites on humans per unit time per human is a/H. If b is the proportion of infected bites on humans that produce an infection, the interaction between the Proportion of susceptible infections recovered Y(t) and the uninfected humans H - X(t) will produce new infected humans of (a/H)b[H -X(t)]Y(t). The incubation period in a human has duration t1; it is possible that some individuals recovered from parasitemia during this incubation period (Smith and McKenzie, 2004). Thus, of those individuals infected t1 unit times ago, only a proportion (a/H)b[H - X(t - t1)]Y(t - t1)e-rt1 is infectious at the present time t, where r is the per capita rate of recovery in humans so that 1/r is the duration of the disease in humans. Therefore, the equation for the rate of change in the number of infected humans

People who have malaria usually suffer chill, fever, sweating, and headache, and may develop severe complications such that they need to seek medical care in hospitals or take breaks at homes. Hospital or home stay plus health education campaign could reduce patient exposure to mosquitoes. In countries approaching malaria elimination,
The stated variables and parameters used for the transmission model are described as the follows;
x(t)Proportion of infected humans
y(t) Proportion of susceptible infections recovered
m ratio of mosquitos to humans
a biting rate on a human per mosquito
b infected mosquito to human transmission efficiency
c infected human to mosquito transmission efficiency
r per capita human recovery rate
μ per capita mortality rate of mosquitos
t1 incubation period for P. vivax in humans
t2 incubation period in mosquitos 5-15 days




In this section we used the model formulated in equation three to compute the result at various times and the result obtained can be discuss to enable used depict the epidemic or otherwise from equation, using defined parameters a represented in the table 1.0 and table 1.1 shows the values of some parameters collected from general hospital Damaturu Local Government, Yobe State on six sep, 2021. We will vary the key parameters to investigate the impact of vaccination on the transmission dynamics of Malaria using pictorial representation (Graphs obtained from the tables).
Table 0.1: Variables and parameters
| Parameters and | Dependent Variable | Values | References |
| Variable | |||
| x(t) | proportion of infected humans | ||
| y(t) | proportion of susceptible infected recovered | ||
| Parameters and Constants | |||
| m | ratio of mosquitos to humans | 2 | [1,2] |
| a | biting rate on a human per mosquito | 0.2-0.5/day | [3, 4, 10] |
| b | infected mosquito to human transmission efficiency | 0.5 | [5, 6, 10] |
| c | Infected human to mosquito transmission efficiency | 0.5 | [5, 6, 10] |
| r | per capita human recovery rate | 0.01-0.05/day | [3, 6, 7, 10] |
| μ | per capita mortality rate of mosquitos | 0.05-0.5/day | [3, 6, 7] |
| τ1 | incubation period for P. vivax in humans | 10-100days | [8, 9, 10] |
| τ2 | incubation period in mosquitos | 1-15days | [3, 9] |
Table 1.1: The initial values and parameters are presented constant
| Case | m | a | b | c | r | μ | τ1 | τ1 |
| 1 | 2 | 0.2 | 0.5 | 0.5 | 0.05 | 0.05 | 15 | 9 |
| 2 | 2 | 0.3 | 0.5 | 0.5 | 0.04 | 0.2 | 18 | 12 |
| 3 | 2 | 0.4 | 0.5 | 0.5 | 0.03 | 0.3 | 21 | 15 |
| 4 | 2 | 0.5 | 0.5 | 0.5 | 0.02 | 0.4 | 24 | 18 |
| 5 | 2 | 0.5 | 0.5 | 0.5 | 0.01 | 0.5 | 29 | 21 |
Table 1.2.0: To shows the Susceptible Infected, and Infectious, Time Period from 2020-2021
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| x | 70,000 | 90,000 | 100,000 | 130,000 | 170,000 | 2,000,000 |
| y | 25,000 | 54,000 | 72,000 | 84,000 | 93,000 | 100,000 |
Table 1.2.1: To shows the Susceptible Infected, and Infectious, Time Period and Parentage
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| x | 70% | 90% | 100% | 130% | 170% | 200% |
| y | 25% | 54% | 72% | 84% | 93% | 100% |




Figure 1: Plot for case 1 Susceptible Recovered, Time Population Fraction
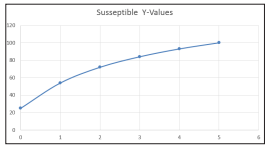
From table1, based on figure1, there is a decline in the number of non-infected person in the society of Damaturu Local Government host, although, the number of non-infected decline steadily and latter increase sharply showing in the community
Figure 2: Plot for case 2 Infected Recovered, Time Population Fraction
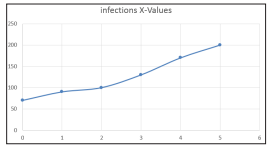
From table, based on figure2, there is a decline in the number of infected person in the society of Damaturu Local Government Yobe State host, although, the number of infected decline steadily and later increase sharply showing the community
Figure 3: Plot for case 3 incubations period in a human
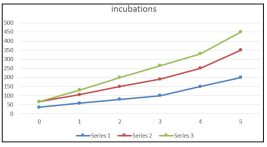
From table 3, based on figure 3, there is a decline in the number of incubation in Human and Mosquitos in the society of Damaturu Local Government Yobe State host, although, the number of incubation in Human and Mosquitos decline steady and latter increase sharply showing a threat to the community

However, the table 3 and table 2 the above figure 1 depicts that an epidemic has set up and the level of the epidemic is totally of the final stayed affecting on average of 75,000. People in just four months, that is it infected positive is steady from the onset and letter it exponentially increase causing every large to the society. Also the graph below depicted the non-infected people against the time in the same society of host at that period in time
Based on the findings so far, Vector insect generates series which converge speedily after some iteration. The epidemic has set up affecting the positive fraction of the community in Damaturu host with as average of 75% infected person pare Month. The epidemic level was slow in the first place but later it increases exponentially indicating a sign of danger to the said community of host.
Sequel to the finding obtained in this study it is obvious that the results obtained have depicted the number of people likely to be infected over a period of time and make a reasonable for best of how many people to be infected in a certain time to enable a proper decision and supply in case of an spread of Vector insect (Malaria) is a contagious bacterial like this in a given society of host with not known in the population number.
Although the study has not make it to our consumption the death that occurred since inception of the epidemic the number of recovered people and the inclining and declining, in the trend of their immune system during Malaria when on treatment. Further study could be conducted by any interested candidate to make clarification of these not known parameter enlisted above by the study
A study of this nature need data from the host societies which were normally monitored and checked by health agencies difficulties is often encountered while trying to collect the data for the paper. In conclusion I would like to say that since there is an outbreak in the said society of host a special care unit be built by the government in at least every unit of local government so that we can get proper health care.
