Author(s): <p>V G Plekhanov</p> <p> </p>
The non - accelerator observation of the long - range strong nuclear interaction is presented. We have studied the low - temperature spectra (reflection and luminescence) of the LiH (without strong interaction in hydrogen nucleus) and LiD (with strong interaction in deuterium nucleus) crystals which are different by term of one neutron from each other. The experimental observation of isotopic shift (103 meV) of the phononless free excitons emission line in LiD crystals is a direct manifestation of the long - range strong nuclear interaction. Such conclusion is made to the fact that the gravitation, electromagnetic and weak interactions are the same in both kind crystals, it only emerges the strong interaction in deuterium nucleus. As far as Born - Oppenheimer approximation does not work in isotope effect, we tentative connect our experimental observation with long - range hadron - lepton interaction. Most important study of the LiHxD1-x mixed crystals is the first measurement of the long - range force dependence of strong nuclear interaction on the distance between nucleons in deuterium nucleus
Subatomic physics deals with the study of the elementary constituents of matter and the interaction between them. Nuclear and elementary particles physics are essentially at the forefront of nowadays understanding of physics. Nucleus is a bound system of strongly interacting protons and neutrons (more generally baryons and mesons - this is the reason for the collective name hadrons) holds atomic nuclei together and, in another context, binds quarks within hadrons. The baryons are bound states of three quarks and mesons are composed of quark and antiquark (see, e.g.) [1]. It should be add that the forces between the quarks must be long - range, because the gluons (as photons) have zero mass. Traditionally the forces between hadrons are short - range and the residues of the for as between their quark constituents (see, also) [2]. As was indicated above nucleus is a bound system of strongly interacting protons and neutrons. Unfortunately, modern Quantum Chromodynamics (QCD) (the modern theory of strong interaction) does not provide us with the tools to calculate the bound states of the proton (deuteron) from first principles (see, e.g.) [3].
As we all know in 1932 the neutron (n) was discovered and the modern atomic structure was complete with massive nucleus consisting of protons (p) and neutrons surrounded by a “cloud” of light electrons [2, 4]. The discovery of the neutron by Chadwick in 1932 may be viewed as the birth of the strong nuclear interaction: it indicated that nucleus consists of protons and neutrons and hence the presence of force that holds them together strong enough to counteract the electromagnetic repulsion [4]. In 1935 Yukawa have tried to develop a theory of nuclear forces. Yutaka’s potential has the form

for some n [5]. Here the strength of the force is measured by the constant k (see, also) [2]. The most important feature Yukawa’s forces is that they have a small range (~ 10 -15 m). The central dogma of atomic physics after Yukawa’s paper that proton - electron attraction could be explained in terms of classical electrostatic theory, while the strong force effects were essentially new and inexplicable. So, far the best theoretical guess is the Yutaka potential, but it is a static potential not dependent on velocities of the nucleons. A static force is not a complete one because it can not explain the propagation of the nuclear interaction. Moreover, phenomenological Yutaka potential can not be directly verified experimentally. We should note that nowadays in text books and elsewhere the separation of electromagnetic and strong interaction tacitly assumed. It is very strange up to present time we do not even know the strong force very well. And what is more we have some contradiction taking into account that the forces between quarks must be long - range, because the gluons have zero mass. But as was mentioned above the force between colorless hadrons is short - range, when the distance between hadrons is more than nuclear size [1]. We can see that the border of the nuclear size transforms long - range interaction in the short - range one. It is very old question which up to present time has not any theoretical explanation.
Obviously we should remember that all structure nucleus and nucleons are a successful experiments in scattering different particles. However performing scattering experiments would not be enough to study the laws of subatomic physics (see, also) [6]. Therefore discovering new methods, besides scattering, would be beneficial for such study. Recently we have shown the experimental manifestation of the strong nuclear interaction in solids and presented it in a series of international conferences on high energy physics [7, 8]. The present paper devoted to, firstly, experimental manifestation of the long - range nuclear strong interaction and secondly, the nuclear strong force dependence on nucleons’ distance in between.
The main experimental results were obtained on devices used already in the earlier investigations [7-10]. For clarity, we should mentioned here that the experimental method involving home - made helium cryostat and two identical double - prism monocromators as well as photoelectrical recording system with signal accumulation in the memory of personal computer. For measuring the luminescence spectra the crystals were excited by the light from mercury (250 W) and deuterium (400 W) lamps.
In our experiments we investigated two kinds of crystals (LiH and LiD) which are differ by a term of one neutron. Lithium hydride and lithium deuteride are ionic insulating crystals with simple electronic structure, four electrons per unit cell, both fairly well -- described structurally (neutron diffraction) and dynamically (second -- order Raman spectroscopy) and through ab initio electronic structure simulation.
Among other arguments, LiH and LiD are very interesting systems due to their extremely simple electronic and energy structure and to the large isotopic effects when the hydrogen ions are replaced by the deuterium ones.
The single crystals of LiH and LiD were grown from the melt by the modified method of Bridgeman - Stockbarger (see and references quoted therein) [8, 11]. The crystals were synthesized from 7 Li metal and hydrogen of 99.7% purity and deuterium of 99.5% purity. Virgin crystals had a slightly blue - grew color, which can be attributed to nonstoichiometric excess of lithium present during the grown cycle. On annealing for several days (up to 20) at 500°C under ~ 3 atm of hydrogen or deuterium, this color could be almost completely eliminated. Because of the high reactivity and high hygroscope of investigated crystals an efficient protection against the atmosphere was necessing. Taking into account this circumstance, we have developed special equipment which is allowed to prepare samples with a clean surface cleaving their in the bath of helium cryostat with normal or superfluid liquid helium [9]. The samples with such surface allow to perform measurements during 15 hours. An improved of LiH (LiD) as well as mixed crystals were used in the present study. In spite of the identical structure of all free - exciton luminescence spectra, it is necessary to note a rather big variation of the luminescence intensity of the crystals from the different batches observed in experiment.
Before beginning a general discussion of long - range strong nuclear interaction, it is helpful to have an idea of electronic structure of bulk materials. As is well - known the nature of materials is determined by the interaction of their valence electrons with their charged nuclei and core electrons. This determines how elements react with each other, what structure the solid prefers, its optoelectronic properties and all other aspects of the material. The modern view of solid state physics is based on the presentation of elementary excitations, having mass, quasiimpuls, electrical charge and so on [12]. According to this presentation the elementary excitations of the non - metallic materials are electrons (holes), excitons (polaritons) and phonons. The theory discussed in modern text books (see, e.g.) forms the basis for the modern theory of electrons in solid [13]. It arises from the consideration of the periodicity of the crystal structure. This periodicity leads to the formation of energy bands (see Fig. 1). The importance of the electronic theory of solids as embodied in band theory is that it provides us with clear means of understanding how solids may be insulators, semiconductors, or metals. This depends upon whether or not it is Fermi surface. The existence of a Fermi surface produces metallic behavior, whereas at 0K, if the filled electron levels (bands in solids - see Fig. 1) are separated from vacant ones, we have insulating properties. The difference between a good conductor and a good insulator is striking. The electrical resistivity of a pure metal may be as low as 10-10 ohm-cm at a temperature of 1 K, apart from the possibility of superconductivity. The resistivity of good insulator may as high as 10²² ohm-cm. The understand the difference between insulators and conductors, we shall use the band -- gap picture ( Fig. 1). The possibility of band gap is the most important property of solids.
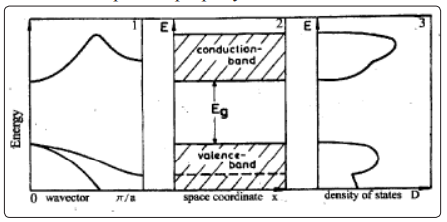
Figure 1: Various possibilities to present the band structure of homogeneous undoped insulator (semiconductor). 1 - the dipersion relation, i.e. the energy E as a function of the wave vector k, 2 the energy regions of allowed and forbidden states as function of a space coordinate x and 3 - the density of states (all curves are schematic ones).
Free exciton luminescence is observed when LiH (LiD) crystals are excited in the midst of the fundamental absorption. The spectrum of free exciton photoluminescence of LiH crystals cleaved in superfluid helium consists of a narrow (in the best crystals, its half - width is ΔE ≤ 10 meV) phononless emission line and its broader phonon repetitions, which arise due to radiated annihilation of free excitons with the production of one to five longitudinal optical (LO) phonons (see Fig. 1 in Reference) [7b ].
The phononless emission line coincides in an almost resonant way with the reflection line of the exciton ground state which is indication of the direct electron transition X1 - X4 of the first Brillouin zone [8].The lines of phonon replicas form an equidistant series biased toward lower energies from the resonance emission line of excitons. The energy difference between these lines in LiH crystals is about 140 meV, which is very close to the calculated energy of the LO phonon in the middle of the Brillouin zone.
The isotopic shift of the zero - phonon emission line of LiH crystals equals 103 meV. As we can see from Fig. 1 (Reference) the photoluminescence spectrum of LiD crystals is largely similar to the spectrum of intrinsic luminescence of LiH crystals (see, also Fig. 2) 7b . There are, however, some distinctions one is related. Firstly the zero - phonon emission line of free excitons in LiD crystals shifts to the short - wavelength side on 103 meV. These results directly show the violation of the strong conclusion that the strong force does not act on leptons. The second difference concludes in less value of the LO phonon energy, which is equal to 104 meV. The simplest approximation, in which crystals of mixed isotopic composition are treated as crystals of identical atoms having the average isotopic mass, is referred to as virtual crystal approximation (VCA) [14].
When light is excited by photons in a region of fundamental absorption in mixed LiHx D1-x crystals at low temperature, line luminescence is observed (Fig. 2), like in the pure LiH and LiD crystals. As before, the luminescence spectrum of crystals cleaved in superfluid liquid helium consists of the relatively zero - phonon line and its wide LO replicas [14]. For the sake of convenience, and without scarfing generality, Fig. 2 shows the lines of two replicas. Usually up to five LO repetitions are observed in the luminescence spectrum as described in detail in [8]. In Fig. 2 we see immediately that the structure of all three spectra is the same. The difference is in the distance between the observed lines, as well as in the energy at which the luminescence spectrum begins, and in the half - width of the lines.
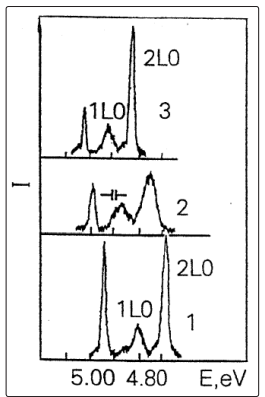
Figure 2: Photoluminiscence spectra of free excitons in LiH (1), LiHx D1-x (2) and LiD (3) crystals cleaved in superfluid helium at 2 K. Spectrometer resolution is shown
The measurements of the low temperature of reflection and luminescence spectra of the whole series of mixed crystals is permitted to obtain the dependence of the interband transition (the long - range force dependence of strong nuclear interaction on the distance between nucleons in deuterium nucleus) energy on the deuterium concentration (Fig. 3) [8]. This dependence has a nonlinear character. As can be seen from Fig. 3, VCA method (the straight dashed line) cannot describe observed experimental results.
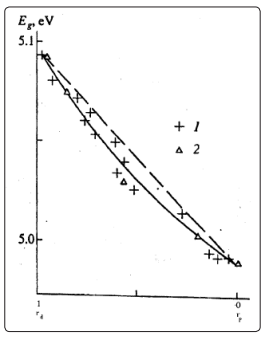
Figure 3: The force dependence of strong nuclear interaction on the distance between nucleons in deuterium nucleus. The straight dashed line is the linear dependence of the force dependence Fs = f(x) in the virtual model. The solid line corresponds to calculation using the polynom of second degree Fs = f(rd ). Points derived from the reflection spectra indicated by crosses, and those from luminescence spectra by triangles.
Comparison the experimental results on the luminescence (reflection) and light scattering in the crystals which differ by a term of one neutron only is allowed to the next conclusions [8]; 1. At the adding one neutron (using LiD crystals instead LiH ones) is involved the increase exciton energy on 103 meV. 2. At the addition one neutron the energy of LO phonons is decreased on the 36 meV, that is direct seen from luminescence and scattering spectra. Both characteristics are macroscopic.
Traditionally nuclear - electron interaction (in our case neutron - electron interaction) taking into account the solving of Schrödinger equation using Born - Oppenheimer (adiabatic) approximation [16]. Since electrons are much faster and lighter than the nuclei by a factor nearly 2000 the electron charge can quickly rearrange itself in response to the slower motion of the nuclei, and this is the essence of the Born - Oppenheimer approximation. This approximation results the omission of certain small terms which result from the transformation. As was shown in the eigenvalue (energy) of the electronic Schrödinger equation (equation 6 in [16]) depends on the nuclear charges through the Coulomb potential, but it doesn’t include any references to nuclear mass and it is the same for the different isotopes (more details will be published separately) [15]. The independent of the potential energy (the eigenvalue of the Schrödinger equation) is the essence adiabatic approximation. However, we must repeat, that the Born - Oppenheimer approximation is the standard anzatz to the description of the interaction between electrons and nuclei in solids (see, e.g.) [15, 16]. The last result is forcing us to search for new models and mechanisms of nuclear - electron interaction including results of subatomic physics, e.g. hadron - lepton interaction.
Out of four known interactions, three are described by SM - the electromagnetic, weak and strong ones [17]. The first two of them have a common electroweak gauge interaction behind them. The strong interaction in SM is described by the QCD, a theory with the gauge group SU(3)C. The effective coupling constant of this theory grows when the energy decreased. As a result, particles which feel this interaction cannot exist as free states and appear only in the form of bound states called hadrons (see, also) [1]. Most of modern methods of quantum field theory work at small values of coupling constant, αs, that is, for QCD, at high energies. Quarks and leptons, the so - called SM matter fields, are described by fermionic fields [18]. Quarks take part in strong interactions and compose observable bound state hadrons. Both quarks and leptons participate in the electroweak interaction. The matter fields constitute three generation: particles from different generation interact identically but have different masses (see, e.g.) [2, 15]. The gauge bosons, which are carriers of interactions, are massless for unbroken gauge groups U(1)EM (electromagnetism - photons) and SU(3)C (QCD - gluons), masses of W± and Z° bosons are determined by the mechanism of electroweak symmetry breaking [3]. It should be noted that the forces between the quarks must be long rang, because the gluons have zero mass. This does not imply that forces between hadrons are also long range, because hadrons have zero color charges overall. The forces between the colorless hadrons are the residues of the forces between their quark constituents, and cancel when the hadrons are far apart.
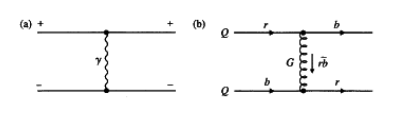
Figure 4: Comparison of the Feynman diagrams of electromagnetic (a) and strong (b) interactions. The electromagnetic interaction in (a) involves two types of electric charge, (+) and (-) is mediated by an uncharged photon. In (b) the strong interquark force involves six types of color charge. The diagram depicts the interaction of a red quark with a blue quark via the exchange of a red - antiblue gluon.
The diagram of Fig. 4 is drawn for the case of single -- gluon exchange, but taking into account that strong constant coupling αs ~ 1, multiple exchanges, involving terms αs ², αs ³, .... must also be very probable. However, it turns out that for violent ‘close’ collisions at very high q², αs <<1 and single - gluon exchange is a good approximation, while at low q² or, equivalently, larger distances, the coupling becomes very large and the theory is incalculable (see also) [3, 8, 19]. This large - distance behavior is presumably linked with of confinement of quarks and gluons inside hadrons. Since gluons are massless, one might expect the static QCD potential to have a similar 1/r, form to that in QED. In fact the quark - antiquark potential is often taken to be of the form [3].

The factor 4/3 in (3) is plausible in view of the fact that there eight color gluon states, to be averaged over three quark colors, giving factor 8/3 as compared with QED (one ‘color’ of photon and one fermion charge). This has to divided by 2 because, for historical reasons [3], a factor 2 enters into definition of αs in terms of the square of the strong color charge. However, at larger distances the second term in (2) is dominant and is responsible for quark confinement. The value of k is about 0.86 GeVfm- 1. In equation (2) the attractive force at large r is dV/dr = k = 0.85 GeVfm- 1 [19]. The estimation of the value of k = 13.9 tones weight - a great deal for those tiny quarks, each weighing less than 10-24 gm. Because gluons carry a color charge (unlike photons which are uncharged) there is a strong gluon - gluon interaction.
Returning to our non - accelerator experimental results, we should underline that in this paper we measure the long - range strong nuclear interaction in crystals which differ by term of one neutron from each other. When we add one neutron in the hydrogen nucleus, we artificial activated of the strong nuclear interaction. As far as the gravitation, electromagnetic and weak interactions are the same in both kind crystals (LiH and LiD), it only emerges the strong interaction. Therefore a logical conclusion is made that the renormalization of the energy of electromagnetic excitations (isotopic shift equals 0.103 eV) is carried out by strong nuclear interaction. The short range character of the strong interaction of nucleons does not possess direct mechanism of the elementary excitation (electrons, excitons, phonons) energy renormalization, which was observed in our low temperature experiments. Second reason that the interpretation of our experimental results is very difficult task because they are first demonstration of the violation of the strong conclusion in nuclear and particles physics that the strong nuclear force does not act on the colorless leptons (see, e.g.) [1, 18]. Similarly on quarks potential we should suppose that the potential of strong nuclear interaction has the next form:

where the first term is Yukawa’s short - range potential, and the second term which has a long - range character of interaction and depends on the distance (r) between nucleons in deuterium nucleus. Our tentative interpretation supposes that the origin of the second term in equation (4) is due the magnetic - like long - range interaction (see also) [21]. This assumption is in accordance with very large value magnetic moment of neutrons (see, also) [2, 20]. Moreover, as we can see from results of Fig. 3 the force dependence of strong nuclear interaction on the distance between nucleons in deuterium nucleus has a nonlinear character. We should stress that this is the first observation in experiments the long - range force dependence of strong nuclear interaction on the distance between nucleons in nucleus. An another possible interpretation of our experimental results is to take into account that in addition to the 8 gluons predicted by QCD SU(3)C group there is a ninth gluon color singlet as photon and may interacts with colorless hadrons and leptons [1].
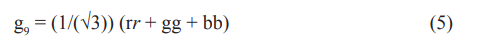
where r,g, b are antiquarks. This massless photon like gluon may be strongly interacts between nucleons (neutrons) and leptons (electrons) [1, 3].
The artificial activation of the strong nuclear interaction by adding one (two or more) neutrons in atomic nuclei leads it to the direct observation of the long - range strong interaction in low - temperature optical spectra of solids. This conclusion opens new avenue in the investigation of the constant of strong nuclear interaction in the wide value range by means the condensed matter alike traditional methods. We should stress that this is the first observation in experiments the force dependence of strong nuclear interaction on the distance between nucleons in nucleus. Our experimental non - accelerator results may shed light on a number of fundamental puzzles in modern physics, particularly on the unification of forces taken into account long - range strong force. Experimental observation of the renormalization of the elementary excitation energy of solids by the strong nuclear interaction stimulates its count in the process of description of the elementary excitations dynamics in quantum electrodynamics. Besides, we should highlight that such important information has been obtained via rather simple and inexpensive experimental physics equipment.
Many thanks to Dr. K. Walker for reading my manuscript, G. Tumar and G.A. Plehhanov for improving my English.
