Author(s): Mihai Oane*, Gabriela Craciun, Elena Manaila, Daniel Ighigeanu
The intense laser irradiation of a micro/nano size W sphere sample is considered in the present paper. Like numerical example, we choose a sphere with a radius of 1 µm. The present article’s point consists of approximating that the target’s temperature homogenization time is of the same order of magnitude as the first laser pulse duration. Our model is valid in the radius limits: 10 nm to 10 µm. We consider like heating source a laser beam with YAG/Nd:YAG/ Cr4+:YAG composite crystal. The nature of the interaction between a laser beam and small dimension tungsten (W) sample is of great importance for both theoretical and experimental perspectives. In principle, we have three stages: i) laser- W bulk interaction; ii) plasma formation, heating, and iii) adiabatic expansion. In the present paper, we will focus on the first two stages of laser pulse interval.
As we already mentioned in the abstract, the present paper’s main approximation is that the target temperature homogenization time is of the same order of magnitude as the first laser pulse duration (order of magnitude of nano-seconds) [1]. We have two heat transfer models whose information could be mix to obtain more realistic modeling. In the first model, we do the main calculations based on determining the sphere’s energies considering the different phase transitions. In the second model, we initially do not consider the phase transitions [2-4]. Still, we estimate the energies obtained in simple laser- solid target interaction to conclude if we have enough power to make the phase transition. Finally, we corroborate the information from both approaches, in the idea to have a very accurate model, which could be useful infusion applications.
Because the target dimensions are considered very small (up to a sphere of 1 μm radius), one laser pulse energy is enough to produce W fusion. For a sphere of diameter 100 nm, the temperature homogenization time drops to 10-7 s = 100 ns.
From the very beginning, we want to point out that from physical reasons: the small dimensions of the sample and the short laser pulse duration; we can consider for laser-W bulk interaction that the entire bulk matter has the same temperature until reaches the melting temperature of 3695 K. At the melting temperature, due to the same physical reasons as well as the higher incident laserintensity, we may consider that the phase transition takes place in a brief period, simultaneously in the entire W volume which becomes liquid. In other words, the melting process takes place.
For tungsten, the molar volume is about 9.47x10-6 m3 /Kmol. If we considerthe radius of about 1 μm, the number of moles is:
N = 4 x ? x (10 - 6) 3 / (3x9.4x10 - 6) K moles = 4.4232 x 10 -10 moles. (1)
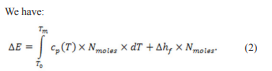
For the values of cp (T) we used the White-Minges fit in the range: 300 < T (K) < 3080, the Wilthan fit in the range 3080 < T (K) < 3695 and the Wilthan value for T (K) > 3695:
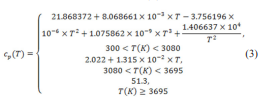
In equation (3), cp (T) is expressed in J/ (mol K) and is the W latent heat of fusion. Our estimations give the necessary energy to reach the fusion point of 3695 K (equations: (1), (2), and (3)): 50.8648 μJ and the energy necessary to make the transition from solid to liquid phase: 23.1333 μJ. In other words, the total energy to obtain the fusion of the W sphere is: 73.9981 μJ
We can also calculate the energy necessary to reach the vaporization point of 6000 K, for the same W target, (starting from the fusion point of 3695 K.), which has the value: 52.3028 μJ. It is beyond the scope of the present paper, but we only want to mention that the inverse Bremsstrahlung process plays a major role in heating plasma electrons by laser radiation. From a classical viewpoint, the electron oscillates in the electric field of the laser beam. During a collision with the nucleus, the electron is knocked out of phase with the electric field. Due to this collision, the oscillatory energy of the electron is converted to random thermal energy.
It is the case to apply the second heat transfer modeling for laser- (solid/liquid) interaction. For this purpose, we use the Goldenberg and Tranter (1952) heat transfer model between laser beam and W sphere. We consider the W sphere to be uniformly heated by the laser beam [4-6]. The W target is placed in an infinite homogeneous medium that we will consider being a He surrounding fluid.
If we define:r- = R - dr; r+ = R + dr; dr ?0, (R is the radius of the W sphere) we may calculate:
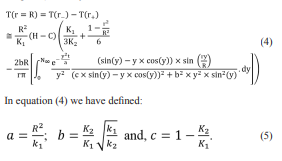
Here, H represents the heat rate per unit time per unit volume generated by the W sphere during its interaction with the laser pulse; C represents the cooling rate per unit time per unit volume generated by the W sphere during its interaction with the liquid He.K1 , K2 , k1 , k2 are the thermal conductivities and diffusivity of the W target sphere and the He liquid surrounding medium, respectively. For W we have the following numerical values: K1 =174 W/mK, k1 =7x10-5m2 /s, pW=1925Kg/m3 and for He: K2 =0.142 W/mK, k1 =15x10-5m2 /s, pHe=0.1785Kg/m3 .
It was pointed out that the annular beams are efficiently used to improve the lateral resolution. In general, the laser intensity decreases to about 20% after passing through the annular pupil filter. For the circular beams, the lateral resolution could be of about 1 μm [7].
On the other hand, very recently, the realization of a Q-switched YAG/Nd:YAG/Cr4+:YAG pulse burst 1064 nm laser. The pulse length is about 10 ns with a pulse fluence of 0.2 J/cm2 .
To calculate the H and C parameters from equation (4), it is opportune to recall some physical assumptions to simplify our modeling. First of all, we have to point out once again that because of the small dimensions (1 μm radius) of W sphere and of nanosecond time scale of the first laser pulse, is it appropriate to consider that the temperature homogenization time of the target is of the same order of magnitude as the first laser pulse duration [8]. On the other hand, at these input parameters, the thermal penetration depth in solids is about 1 μm, which hypothesizes that the entire target is heated directly. Therefore, almost all incident energy will be transformed into heat. This hypothesis is also in concordance with the temperature homogenization in time and space assumption. If we consider F = 0.2 J/cm2 , Tpuls=10ns, R=10- 6 m, the absorption coefficient Q=0.2, our estimation gives: H - C =1.5 X 1016J /m3 s. Our simulations show (see Fig.1.) that after irradiation with a single laser pulse, the 1 μm radius W sphere reaches the fusion state. Our necessary calculations indicate that the entire process of the mentioned phase transition is about 0.828 ms. It could be a problem with plasma stability. Consequently, we come back to reference and “take advantage” because, in 1ms, we could have 11 identical pulses [6]. A short calculation gives us a fusion time of about 9.108 ms, which is in excellent agreement with our simulations (see Fig.2.). We conclude that just the second simulation is self-consisted because the time irradiation is precisely when the W target has to “win” all the energy necessary for reaching the fusion temperature and for the phase change.
Our study could be of great interest for laser processing of metals in general and W’s analysis in particular [9-12].
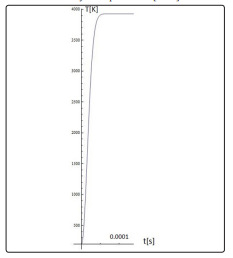
Figure 1: The thermal field in a 1 μm radius W sphere under 1very powerful pulse laser irradiation.
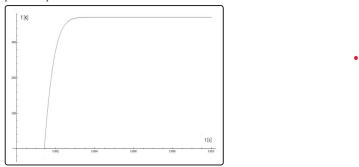
Figure 2: The thermal field in a 1 μm radius W sphere under 11 very powerful pulses laser irradiation
Figs. 1 and 2 show the correlation between the numbers of pulses (in time) with the W sphere’s thermal distribution. It can be analyzed that the number of pulses has no impact over target’s temperature homogenization time and is found to be the same order of magnitude as the first laser pulse duration.
The intense laser irradiation of a micro/nano-sized tungsten (W) sphere sample with 1 μm is considered. The current model is valid in a radius of 10 nm -10 μm. A laser beam source with YAG/Nd: YAG/Cr4+:YAG composite crystal was taken into account. Three stages were discussed: i. laser-W bulk interaction; ii. plasma formation, and iii. adiabatic expansion. However, in this study, only the first two stages of laser pulse interval were discussed.
One can conclude that the nature of the interaction between a laser beam and a small dimension W sample is of great importance for both theoretical and experimental perspectives. The number of pulses has no impact over target’s temperature homogenization time and is found to be the same order of magnitude as the first laser pulse duration.
Conflicts of Interest: The authors declare no conflict of interest.
