Author(s): <p>Robert J. Buenker</p>
The Lorentz transformation (LT) of Einstein's Special Theory of Relativity (STR) leads to the prediction of time dilation and length contraction in moving rest frames. In addition, the relativistic velocity transformation (RVT) is derived from the LT by simply taking the ratios of its space and time coordinates, and this in turn guarantees satisfaction of Einstein's light-speed constancy postulate. The Global Positioning Transformation (GPS-LT) is similar to the LT but differs from it in a significant way, namely it does not lead to the space-time mixing characteristic of the LT. The way in which time dilation is derived from both transformations is compared and it is shown that only the GPS-LT is self-consistent with respect to this key prediction of relativity theory
The Lorentz transformation (LT) is the cornerstone of Einstein's Special Theory of Relativity (STR) [1]. It is the basis for all of STR's predictions about the relationships between space and time. It has led to the revolutionary concept of spacetime, which holds that the two entities are inextricably mixed in physical interactions. It satisfies the two postulates of relativity that were enunciated by Einstein in his landmark paper, namely the Relativity Principle (RP) and the constancy of light in free space. There is another transformation that also satisfies both of these postulates, however, but one which differs from the LT in a very significant way [2- 4]. It is referred to as the Global Positioning System- Lorentz transformation (GPS-LT) because of its close connection to the hugely popular navigation system which has become essential in our everyday life. The GPS-LT holds that space and time are completely separate entities, in agreement with the classical view espoused by Newton in the late 17th century (it is sometimes referred to as the Newton-Voigt transformation or NVT), whereas the LT claims instead that these quantities are inextricably intertwined [5].
Both relativistic transformations lead to the prediction of time dilation, the belief that the rates of clocks vary with their state of motion. Once again, it is found that they differ in a substantial manner, however. The LT claims that the effect is symmetric, that observers in motion with respect to one another will measure a slower rate for the clock in the other's rest frame. Measurement is a subjective process according to this view, possibly just a matter of the perspective of the observer. The GPS-LT on the other hand claims that it is always possible, at least in principle, to know which of two clocks runs slower, that measurement is thoroughly objective in character. Because of this clear distinction, it is instructive to consider how each transformation comes to its prediction of the time-dilation phenomenon. The starting point in this discussion is the definition of both transformations given below.
To illustrate how the two relativistic space-time transformations discussed above are applied in practice, it is helpful to consider the example of two lightning strikes. These events are witnessed by two observers who are moving with speed v relative to each other along the x axis in a mutually agreed upon coordinate system. The elapsed times separating the lightning strikes are designated as ?t’ and ?t, respectively, for the two observers (who are stationary in rest frames S and S', respectively). The corresponding distances between the locations of the lightning strikes are denoted by ?x’ and ?x in the two rest frames. In the Lorentz transformation (LT) the relationship between these various quantities is given by the equation given below:
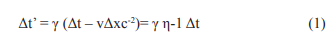
where γ= (1-v2 c-2)-0.5 and c is the speed of light in free space (299792458 ms-1). The corresponding equation in the GPS-LT is completely independent of the distances separating the two lightning strikes, but is rather the simple proportionality relation given below between the respective elapsed times of the two observers:

In this case, Q is a constant which is a unique characteristic describing the relationship between the rest frames of the observers.
In order to derive the time-dilation prediction of the LT, an example is considered in which a stationary clock in one of the rest frames (S') is used to measure the time difference ?t' for the two lightning strikes (or any other pair of events). There is no restriction on the types of events to be considered [6]. The time difference could be a lifetime or an elapsed time of any kind, for example. It is stipulated that the clock remain in the same position during the entire measurement, which means that ?r'2 = ?x'2 + ?y'2 + ?z'2 =0. Use is then made of a characteristic of the LT known as the Lorentz invariance condition. It is obtained by summing the squares of the LT space-time variables (with appropriate definitions of the distance intervals along the y and z directions):

As has been often discussed in the literature, eq. (6) cannot be obtained from eq. (5) by algebraic inversion. Instead, there is a symmetric relationship between the two equations that can be conveniently summarized by noting that it is always the moving clock relative to the observer that runs slower. This is a completely subjective relationship, since it indicates that it is just a matter of perspective which of two moving clocks has the slower rate.
The key point in the present discussion is that the LT time-dilation relationships of eqs. (5, 6) are not consistent with eq. (1) of the LT. For example, the latter indicates that remote non-simultaneity (i.e. ?t'?0 even though ?t=0) occurs whenever v and ?x both have non-zero values. The time-dilation relationships in eqs. (5, 6), by contrast, both state unequivocally that events which are simultaneous for one observer must also be simultaneous for all others because in this case ?t and ?t' are simply proportional to one another. Therefore, if ?t=0, then ?t'=0 as well.
This raises the question as to whether the same lack of consistency occurs for the GPS-LT, in which case it would be clearly necessary to conclude that this transformation is also not physically viable. To check this possibility, we can again consider the above example of two clocks in motion. One difference relative to the LT derivation is that the condition of invariance is not the same for the GPS-LT [2-5]. Instead one obtains the following result by squaring each of its equations and combining:

Rearrangement then again gives eq. (2), which shows that the GPS-LT is indeed self-consistent in this example.
It is ironic that the derivation of the proportionality relation between elapsed times in eqs. (5,6) was not recognized as an irreconcilable failure of the Lorentz transformation because of the incompatibility of this result and the latter's prediction of remote non-simultaneity. It is simply mathematically impossible that two observers could disagree whether a time difference is zero or not at the same time that it is established that their clocks are running at strictly proportional rates.
Moreover, the symmetric relationships in eqs. (5, 6) are also unacceptable. Interchanging the variables in the two equations and changing the sign of the relative velocity of the two rest frames should leave both equations invariant. The Relativity Principle demands this because such a procedure amounts to a simple way to effect the inverse relation for each observer, and the laws of physics are supposed to be the same for both. Because γ retains its value as a result of changing the sign of v, the required invariance does not occur and instead one obtains two different relationships between their elapsed times. According to the theory, it therefore becomes impossible to say for certain which of two clocks runs slower or faster.
Einstein and many generations of physicists along with him nevertheless have held steadfast in their belief that the Lorentz transformation (LT) is the unique mathematical solution to the problem of developing a relation between space and time variables which is consistent with his two postulates of relativity: the constancy of the speed of light, independent of the states of motion of both the observer and the light source, on the one hand, and the Relativity Principle on the other. The discovery of the Global Positioning System-Lorentz Transformation (GPSLT) negates this claim. It also satisfies Einstein's postulates, but it does so while avoiding any contradiction in the derivation of the time dilation phenomenon. Its eq. (6) achieves this objective by demanding that the constant Q change to Q' = 1/Q when the above "physical" inversion procedure is applied to it. One can understand the relationship between Q and Q' by looking upon them as conversion factors between the different units of time employed in the two rest frames. A similar relationship holds for any physical property. The conversion factor in going from m to cm is 100, for example, while that in the reverse direction is 1/100. As a result, the true relativistic space-time transformation conforms to the ancient principle of the objectivity of the measuring process. The GPS-LT also does something else, however. It shows that the mixing of space and time implied by eq. (1) of the LT is not an essential fact of nature. In this respect, Newton was right and Einstein was wrong
