Author(s): Jyoti Bhattacharjee and Subhasis Roy*
Spin dynamics in molecular systems lies at the heart of contemporary research, promising revolutionary applications in fields like spintronics and quantum information processing. The paper provides insights into green techniques to improve spin dynamics for utilization in quantum computing and magnetic materials. This dynamic approach describes the temperature-dependent evolution of spin-lattice interactions. Snapshots acquired from various simulations enable additional DFT investigations, providing a more sophisticated understanding of spin dynamics under temperature variations. By seamlessly integrating theoretical insights with computational approaches, the Density Functional Waltz emerges as a potent paradigm for unraveling the mesmerizing choreography of spin dynamics at the molecular scale. This review analyzes the evolution of machine-learning approaches in the field of chemical sciences. The proposed review will highlight the significance of collaboration between quantum catalysis and the chemical physics community. There is an outline of the unique features of electron spin alongside the ingenious integration of macromolecules to control and fine-tune electron spin-based innovation.
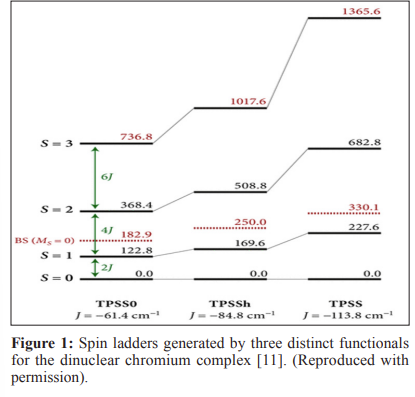
Quantum technologies have emerged as paradigm shifts in various fields, with promising applications in computation, communication, and sensing. Quantum devices that utilize electron spin have received much attention among these technologies owing to their potential for durable and efficient digital processing [1]. This comprehensive review proposal aims to investigate the most recent advances in quantum devices based on electron spin and their manipulation using molecular control techniques. The proposed review will delve into the theoretical framework of Density Functional Theory (DFT) as a strong computational tool for analyzing and forecasting the behavior of molecular systems in the context of spin-based quantum technologies. The first section of the review will begin with an overview of the principles and significance of electron spin as a quantum resource, emphasizing its uses in quantum computing, thermal conduction, vapor adsorption, segregation, storage, thermal catalysis, photocatalysis, biosensors, wireless communication, spintronic circuits, and high-precision perception [2]. Subsequently, this synopsis will portray how Kohn-Sham density functional theory and combined quantum mechanical and molecular mechanical methods can serve as effective platforms for mediating spin interactions, allowing the fabrication of advanced gates and logic operations [3]. The proposed review will include recent studies demonstrating the practical applications of spin-based quantum devices controlled by molecular systems. The paper will include case studies highlighting certain biochemical structures created to fine-tune spin characteristics, which improves device performance and decreases decoherence effects [4]. Furthermore, research gaps exist governing spin-molecule networks in accurately modeling electron spin dynamics within a molecular context, with implications for the stability and coherence of quantum states [5-6]. To bridge these gaps, this review will present new proposals and green methodologies for solving the problems associated with spin-based quantum gadgets and atomic physics. The potential of hybrid systems in which quantum dots or defects inside molecular structures are employed to confine, optimize, and modify photon spins is emphasized. The second section discusses the evolution of machine learning approaches for the last five years to improve the accuracy of DFT calculations and anticipate spin-molecule couplings. The comprehensive overview will focus on the various uses of quantum devices in science, medicine, and engineering, like tunable spin qubits, smart dust, hydrogen batteries, and ultra-sensitive sensors, capable of detecting minute changes in physical, thermoelectric, and chemical properties possible in science [7]. The review will outline the underlying mechanisms responsible for magnetoelectric coupling in composite nano-thin films, including strain-mediated and magnetostrictive-mediated mechanisms, emphasizing how these methodologies emerge from interactions between the magnetostrictive and piezoelectric phases [8]. The paper will address the notion of using spin qubits for quantum-enhanced nuclear magnetic resonance (NMR) spectroscopy, the design of molecular spintronics devices for graphene-based electronic olfaction sensors, and the practical use of quantum algorithms for efficiently addressing environmental pollution [9]. This comprehensive review proposal aims to shed light on the ethical and societal consequences, as well as recent advancements, in data engineering and chemical physics, driven by the effect of macromolecules and influenced by the synergy between DFT and machine learning [10]. These minuscule entities, similar to tiny magnets, have a quantum mechanical feature known as spin, which gives them inherent angular momentumand magnetic moment. Spins in the quantum realm can take on definite orientations, commonly called "up" and "down" or spinup and spin-down. For example, consider a molecular ensemble teeming with activity, where electrons bounce between orbitals and spins perform elaborate ballet. The Density Functional Theory serves as our guiding light here, giving a framework for understanding the dynamic interaction between electronic spins and their surroundings. At its core, DFT provides a rigorous yet elegant way to describe the electrical structure of molecules, with electron density serving as the primary protagonist. Figure 1 gives an overview of the Broken-Symmetry Density Functional Theory (BS-DFT) findings, displaying the energy of the Broken-Symmetry (BS) solution concerning the projected spin states. In simpler terms, in real-world scenarios, the S2 expectation values for the high-spin and broken-symmetry solutions are typically around 12 and 3, respectively. The bond lengths between Cr and O(H) atoms also seem to be a bit longer, averaging around 0.02 Å. This slight increase in length is consistent across different functionals. As a result of these changes, all functionals predict lower values for the exchange coupling constant. However, it's worth noting that generalized gradient approximation (GGA) functionals still tend to overestimate the strength of antiferromagnetic coupling.
When it comes to understanding the electronic and magnetic properties of materials, we have to consider both the electrons' behavior and the atoms' arrangement in the lattice. These properties, known as electronic and magnetic properties (EMPs), become particularly important at finite temperatures [11]. Describing EMPs involves choosing the right level of theory to explain how electrons interact with each other. This could be through simplified mean-field approaches or more complex many-body methods. On the other hand, understanding the spin and lattice configurations requires knowledge of the specific spin arrangements, like whether they are antiferromagnetic (AFM) or paramagnetic (PM), and if there's any short-range order present. We also need to consider the lattice structure itself, which includes any atomic displacements or symmetry breaking that might occur, especially at different temperatures.
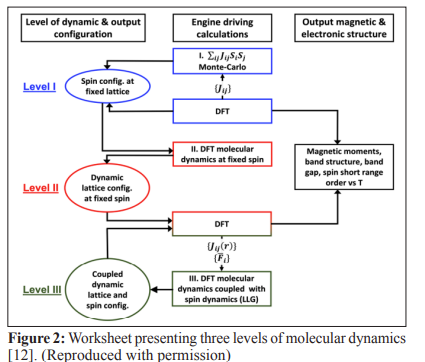
As depicted in Figure 1, across all dynamics levels, the Heisenberg Hamiltonian is utilized (taking into account noncollinear magnetization) to elucidate the interaction between spins and subsequently determine the spin configurations [13]. The Heisenberg Hamiltonian is solely characterized by the orientations of the moments μ i and the spin-exchange interactions J g j:
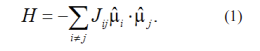
This constitutes the fundamental framework of the Hamiltonian. However, advancements have been made to incorporate additional factors, such as the distance-dependent nature of exchange interactions, longitudinal spin fluctuations, and higher-order terms [13-15]. While the Heisenberg Hamiltonian can effectively simulate spin waves in materials, it faces challenges, particularly concerning the behavior of magnetic materials at low temperatures (e.g., specific heat at low temperatures) and antiferromagnets in specific [16]. Nevertheless, the generalized Heisenberg Hamiltonian facilitates a microscopic portrayal of the principal characteristics of magnetic degrees of freedom (m-DOF).
The Heisenberg Monte Carlo (MC) simulations are conducted at various temperatures, with exchange interactions computed using the equilibrium lattice parameter at 0 K. The exchange interactions outlined in Eq. (1) have been determined utilizing the cluster expansion structure inversion method, incorporating 10 ordered magnetic structures [17].
Separating the EMPs from the spin and lattice configurations has been challenging in this field. Traditionally, theories focusing solely on the behavior of electrons have treated the lattice as a passive observer, almost like a background decoration [18]. However, EMPs and the spin/lattice arrangements are deeply interconnected. Changes in one can significantly impact the other, creating a back-and-forth interplay like a game of ping-pong. For example, lattice structure or spin configuration adjustments can drastically alter the predicted EMPs, and vice versa.
Furthermore, how one models electron interactions to predict EMPs can influence the resulting spin and lattice configurations. Understanding one aspect necessitates considering the other, highlighting the intricate and interconnected nature of electronic and magnetic properties in materials [19]. One crucial aspect of solids is their 'gap,' but defining it isn't straightforward; there are multiple perspectives. First, we can define the gap using concepts like quasielectrons and holes, sometimes called quasiparticles. Imagine trying to pull an electron out of a material-that energy required is called the ionization potential (or work function for metals), denoted as I, and it equals the energy of removing one electron from the system (EN1) minus the energy of the system with all its electrons (EN). We can measure I experimentally using techniques like photoelectron spectroscopy (PES) or inverse photoemission spectroscopy (IPES). The energy needed to add an electron is called the electron affinity, A, which is equal to the energy of adding one electron (EN) minus the system's energy with all its electrons (EN+1). One definition of the gap is the difference between I and A, often termed the physical, quasiparticle, or fundamental gap [20].
In Level III, there is an extension of our analysis by reviewing the pair distance-dependent exchange interactions to capture the coupling between lattice and spin microscopic degrees of freedom. With these interactions determined, we conduct coupled spin and molecular dynamics simulations across various temperatures using ab initio forces. These simulations allow the simultaneous evolution of spin and lattice microscopic degrees of freedom. Snapshots from these joint simulations are then analyzed through further DFT calculations to extract magnetic and electronic structure properties at each temperature [21].
The gap is also associated with excitation energies, as seen in optical spectroscopy. This 'optical gap' is defined by the onset energy of absorption. Optical excitation does not change the number of electrons in the system. Calculating optical properties involves understanding how a quasielectron interacts with a hole and its exchange counterparts. The optical spectrum of a solid relates to the frequency-dependent imaginary part of the macroscopic dielectric function, sometimes calculated using this equivalence [22].
Thirdly, the gap might relate to the energy difference between the highest occupied molecular or crystal orbital (HOMO or HOCO) and the lowest unoccupied molecular or crystal orbital (LUMO or LUCO). This orbital-energy gap is sometimes called the independent-particle, single-particle, or one-electron gap. However, strictly speaking, this gap is only an approximation of the physical or optical gaps. Orbital-energy gaps underestimate physical quasiparticle gaps in semiconductors and insulators [23]. Correcting the orbital energy gap to the quasiparticle one is termed a quasiparticle shift or correction.
Similarly, correcting the physical gap to the optical one is called an exciton shift or local-field effect due to electron-hole interaction. In practice, these corrections can balance out since the quasiparticle shift increases the gap while electron-hole attraction lowers it, similar to how electron-nucleus interactions lower bound states in atoms below the ionization potential. An exciton, a two-body quasiparticle composed of an electron and a hole, arises from this interaction. In materials with weak electron-hole interaction, like semiconductors, excitons spread out over several unit cells (Mott-Wannier excitons). In insulators, where excitons may localize, they're considered mobile, electronically excited states of molecules or formula units (known as Frenkel excitons), and their shift can be significant, often exceeding 1 eV [24].
Relaxation-rate constants play a crucial role in characterizing dynamics in solution-state NMR, with widespread applications [25]. However, their usage in solid-state NMR is less common. The measurement and analysis of longitudinal and transverse relaxation parameters in solid-state NMR, particularly under magic-angle spinning (MAS), pose significant challenges due to both theoretical and experimental factors:
i. In solids, the decay of polarization and coherences involves two components: one due to coherent time evolution under an orientation- and MAS time-dependent Hamiltonian, influenced by non-averaged anisotropic interactions like dipolar couplings, and another due to incoherent processes reflecting dynamics. Isolating the latter, which signifies dynamics, proves difficult in the presence of the former, coherent decay. This presents a major experimental hurdle for measuring transverse relaxation rates and, to a lesser extent, for measuring longitudinal relaxation rate constants. Coherent mechanisms, such as spin diffusion, also impact longitudinal relaxation. In this context, we use "relaxation" to refer specifically to the incoherent decay resulting from dynamics characterized by stochastic processes.
ii. The applicability of Redfield theory isn't automatically assured for transverse relaxation parameters. This is because Redfield's theory assumes that the change in the density operator is negligible compared to the stochastic process timescale, implying that the relaxation-rate constant is significantly smaller than the rate of the dynamic process [26].
iii. Spin relaxation can result from stochastic fluctuations of dipolar couplings, chemical shift anisotropy (CSA) tensors, and isotropic chemical-shift fluctuations (often termed "chemical exchange"). In solution-state NMR, overall tumbling averages dipolar couplings and CSA tensors on a nanosecond timescale, rendering fluctuations of anisotropic interactions on microsecond to millisecond timescales negligible for relaxation. Thus, in solution state, one can distinguish between relaxation due to fluctuations of anisotropic interactions by Brownian tumbling and fast local motions, and slow chemical exchange involving isotropic chemical-shift fluctuations. In contrast, slow motions on micro-to-millisecond timescales in solid-state NMR average both isotropic and anisotropic interactions, necessitating consideration when discussing line broadening and coherence decay [27-28].
In conclusion, the Density Functional Theory is a compelling method for molecular spin dynamics. Since its conception, the Density Functional Waltz has shown amazing versatility and usefulness, particularly in understanding the spin characteristics of materials containing transition metals. Its ability to explain complex spin dynamics at three levels - electronic, spin, and density functional theory dynamics - allows for a thorough knowledge of spin-related events. At Level I, this review sets a foundation with density functional theory calculations that explain exchange interactions on static lattices. These findings effortlessly segue to Level II, where the dynamics of single frozen spin configurations are investigated using ab initio molecular dynamics simulations. This stage yields crucial insights into spinlattice interactions and their effects on electrical and magneticcharacteristics. Finally, at Level III, the investigation reveals its pinnacle as pair distance-dependent exchange interactions, allowing for a better comprehension of the complex interplay between lattice and spin microscopic degrees of freedom. A holistic picture of spin dynamics emerges through joint analysis of these simulations and further density functional theory calculations.
Author (S. Roy) would like to acknowledge ‘Scheme for Transformational and Advanced Research in Sciences (STARS)’ (MoE-STARS/STARS-2/2023-0175) by the Ministry of Education, Govt. of India for promoting translational India-centric research in sciences implemented and managed by Indian Institute of Science (IISc), Bangalore, for their support.
