Author(s): Constantin Fetecau* and Marneni Narahari
The classical solutions of the first problem of Stokes for viscous fluids, as it was to be expected, are obtained as limiting cases of those of the simple Couette flow. Something similar is valid for the motions of the fluids induced by a constant shear stress on the boundary. As a direct consequence, new exact solutions are immediately obtained for other two classes of motions of the same fluids.
The fluid flow over an infinite plate that is suddenly moved in its plane as well as the motion between two parallel plates when one of them slides in its plane is of fundamental theoretical and practical interest it having multiple applications in science and engineering. The first motion is termed Stokes’ first problem or Rayleigh-type flow while the second one is called the simple Couette flow [1-3]. Both motions have been extensively studied in the literature but no connection between their solutions has been established although, if the distance between plates in the case of the simple Couette flow is large enough, the profiles of their solutions have to be almost identical
The main purpose of this paper is to show that the well-known classical solutions
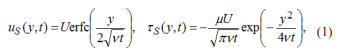
corresponding to the first problem of Stokes for incompressible viscous fluids can be obtained as limiting cases of those of the simple Couette flow. More precisely, we want to prove that
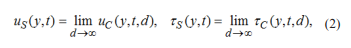
where uC (y, t, d) and ?C (y, t, d) are the velocity field, respectively the adequate non-trivial shear stress corresponding to the simple Couette flow and d is the distance between plates. In addition, for completion, similar relations to those given by Eqs. (2) will be also provided for the motion of incompressible viscous fluids over an infinite plate that applies a constant shear stress to the fluid and the flow between two infinite horizontal parallel plates when the lower plate applies the same constant shear stress to the fluid. To do that, we remember the dimensional velocity and shear stress fields corresponding to the motion of incompressible viscous fluids over an infinite flat plate that applies a constant tangential stress -T to the fluid, namely see for instance Eqs. (4.3) and (4.5) [4].
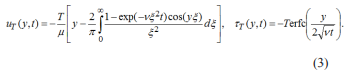
Finally, the obtained results are used to establish connections between the velocity and shear stress fields corresponding to two more general classes of motions of incompressible viscous fluids over an infinite plate or between two infinite horizontal parallel plates. These connections show that the exact solutions corresponding to motions of these fluids over an infinite plate can be well enough approximated by the similar solutions of the flows between infinite parallel plates if the distance between plates increases.
Let us consider an incompressible viscous fluid at rest between two infinite horizontal parallel plates at the distance d apart. At the moment t = 0+ the lower plate begins to move in its plane with a constant velocity U or to apply a constant shear stress -T to the fluid. Due to the shear the fluid is gradually moved and we are looking for a velocity field of the form [5].

in a suitable Cartesian coordinate system x, y and z whose y-axis is perpendicular to plates.
The continuity equation is clearly satisfied while the constitutive relation of viscous fluids and the balance of linear momentum, in the absence of body forces and a pressure gradient in the flow direction, reduce to the relevant partial differential equations
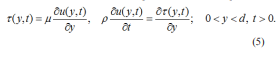
Here u(y, t) is the fluid velocity, ?(y, t) is the non-trivial shear stress, μ is the dynamic viscosity of the fluid and p= μ / v is the fluid density (v being the kinematic viscosity). The appropriate initial and boundary conditions corresponding to the two different motions are
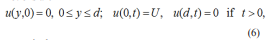
respectively
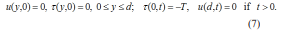
The initial condition ?(y,0)=0 from Eqs. (7) has been included because eliminating u(y, t) between Eqs. (5) we find for the shear stress ?(y, t) a partial differential equation of the same form as that for velocity. Using this condition, the solution (3)2 immediately results.
The dimensional solutions uC (y, t, d) and ?C (y, t, d) corresponding to this problem, as it easy results from [5, Eqs. (9) and (11)] can be presented in the suitable forms

The dimensional velocity and shear stress fields uT p (y, t, d) and ?Tp (y, t, d) corresponding to this motion can be immediately determined from Eqs. (15) and (17) of the reference [5] (1/Re has to be suppressed from Eq. (17) of this reference) that have been obtained using the following non-dimensional variable, functions and parameter.

tend to zero for d? infinity. Furthermore, Figs. 1 clearly show that the profiles of the velocity fields uT (y, t) and vT (y, t) given by Eqs. (3)1, respectively (13) are identical.
Consequently, on the base of these last remarks, we can conclude that
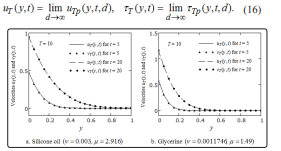
Figure 1: Profiles of the velocity fields μT (y, t) and vT (y, t) given by Eqs. (3)1 and (13)
On the basis of Eqs. (8) and (12) we shall provide similar relations between the velocity and shear stress fields corresponding to other two classes of motions of incompressible viscous fluids over an infinite plate or between two infinite horizontal parallel plates. For this, let us again consider an incompressible viscous fluid at rest over an infinite plate or between two infinite horizontal parallel plates at the distance d apart. At the moment t=0+ the plate, in the first case, and the lower plate begin to move in their planes with the time-dependent velocity Utn where n is a natural number. The expressions of the velocity and shear stress fields un (y, t), ?n (y, t) and unp (y, t, d) ?np (y, t, d) corresponding to these motions, as it results from [6, Eqs. (31) and (32)], respectively [7, Eqs. (31) and (32)] are connected to the previous solutions uS (y, t), ?S (y,t) and uC (y,t,d),?C (y,t,d) by the following relations.

Let us now assume that, in contrast to the previous section, the plate or the lower plate in the case of the motion between parallel plates applies a shear stress -Ttn to the fluid. Denoting by uTn (y, t), ?Tn (y, t) and uTnp (y, t, d), ?Tnp(y, t, d) the velocity and shear stress fields corresponding to the motion over an infinite plate, respectively between parallel plates and using Eqs. (12) and known results from the references [6] and [8] we can easy show that
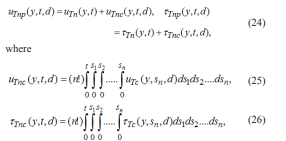
Of course, the fact that the solutions corresponding to the fluid motion between horizontal parallel plates when the lower plate moves in its plane with a constant velocity U or applies a constant shear stress -T to the fluid converge to the similar solutions of the flow induced by an infinite plate that is moving in its plane with the same velocity U or applies the same constant shear stress -T to the fluid when the distance between the two plates tends to infinity is not a surprise and this convergence has been here analytically proved. In addition, the complementary entities uSc (y, t,d) and ?Sc (y, t,d) as well as uTc (y, t,d) and ?Tc (y, t,d) given by Eqs. (9) and (10), respectively (14) and (15) allow us to determine the deviation of the solutions given by Eqs. (8) and (12) from the classical solutions (1), respectively from those given by Eqs. (3). Furthermore, these deviations can be brought to light at each moment of time and for any distance d between plates.
It is worth to point out the fact that the previous results have been used to provide connections between the velocity and shear-stress fields corresponding to the motions of the same fluids induced by the plate (in the case of the motion over an infinite plate) or the lower plate (in the case of the motion between two infinite horizontal plates) which are moving in their planes with a timedependent velocity Ut n or applies to the fluid the shear stress -Ttn . In addition it is easy to verify that all above relations, except that given by the relationship (24)1 , are also valid when porous and magnetic effects are taken into consideration.
