Author(s): Robert J Buenker
The experimental relations between the speeds of galaxies and their corresponding separations from the Earth are discussed in some detail. It is pointed out that Hubble’s Constant, which indicates that the speeds and separations have the same constant ratio for every known galaxy, can be combined with well-known relationships for objects under the influence of constant acceleration to give some concrete predictions of how these quantities vary with time. It is found according to this analysis that the acceleration of each galaxy is directly proportional to its speed, for example. This value is the net result of the continuous competition between gravitational forces and the inertial forces still operative since the Big Bang explosion. Its value is extremely small, equal to only 1.17x10-10 ft/s2 for the Hydra galaxy, for example, which moves at a speed of 38,000 mi/s. Most importantly, the indication is that is that the inertial forces are constantly winning out over the gravitational forces for each galaxy. The resulting equations also indicate that the speed of any galaxy varies in direct proportion to the time Δt which has elapsed since the origin of the universe (Big Bang explosion), while its distance from the Earth varies as the square of this elapsed time. On this basis, it is concluded that Hubble’s Constant itself varies in direct proportion to Δt and thus acts as a “clock of the universe.” More generally, the conclusion from this analysis is that the universe is open and continues to expand outward at an ever increasing rate
There seems to be general agreement among physicists that the universe originated with a massive explosion which has come to be known as the Big Bang. Astronomical measurements carried out at the present time show clearly that the current universe consists of a huge number of galaxies which are moving away from Earth at varying speeds. Edmund Halley in 1720 asked the very basic question of why the sky is dark at night. This was followed by the Olbers’ Paradox, according to which it was argued that the reason the night sky is not filled with light is because the galaxies are constantly in outward motion. Moreover, the universe must be limited in space.
Some two centuries after Halley's question, Edwin Hubble was able to make the theory of the “expanding universe” much more quantitative by measuring the distances separating the various galaxies from the earth. This information was combined with measurements of the red shifts of lines of the same galaxies which were obtained by Hubble's colleague, Milton Humason. From a purely qualitative point of view, these data showed that the galaxies are moving away from the earth, in agreement with the general conclusion of an expanding universe. There was a more quantitatively significant result from the Hubble-Humason collaboration, however. It was found that the ratio of the distance of a given galaxy to its speed relative to the Earth is nearly the same in all cases for which measurements are available. This ratio has come to be known as Hubble’s Constant. It has a value of approximately 105 ly / (mi/s).
Experiment has provided quantitative details of the motion of galaxies which is presently occurring at this point of time in our history. Specifically, we know the distance from the Earth and the corresponding velocity relative to the Earth for a fairly large number of them. Moreover, it is clear from the Hubble-Humason analysis that the ratio H between the distance separating a given galaxy and its speed v in a direction away from the Earth is very nearly the same for each galaxy, at least to a suitably good approximation. Accordingly, when H = 105 is defined as above in standard units of s ly/mi, the distance L is measured in mi and the speed v in mi/s, the following equation can be assumed to be valid to a good approximation :

where X is the number of miles in a light year (5.8786x1012 mi/ly).
The fact that the galaxies are all undergoing acceleration raises the question of how great the acceleration A of a particular galaxy is at the present time. Since HX=L/v in eq. (1) is a constant throughout the universe, it follows that the ratio δL/δv of the local galaxy over a small elapsed time δt will be the same as L/v, i.e. H (or HX) will not change appreciably over this period of time. If attention is centered on a single galaxy, it is therefore possible to use standard formulas which assume a constant acceleration value A away from the Earth when the motion has occurred from a “standing start” at t=0 relative to its current position. Accordingly, the current values of the speed v of the galaxy and its distance from the Earth L can be combined to obtain an estimate of A, as follows.
After time δt has elapsed, on the basis of the standard formulas one obtains a change in speed of δv= Aδt and corresponding change of distance δL=A δt2 /2 relative to their respective current values of v and L, respectively. Elimination of δt then leads to the following relation between A, δv and δL:
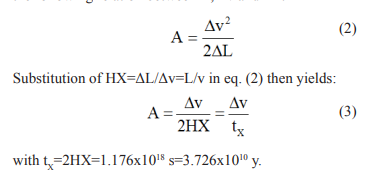
The most obvious way to interpret the above results is simply to assume that t=0 refers to the time of the Big Bang. The first application of eq. (3) to be considered is for the present time frame when the speed of the given galaxy has reached its current value of v, i.e. it is assumed that δv=v. As an example, consider the galaxy Hydra, which is known to have a speed of approximately 3.8x104 mi/s. Substitution of this speed gives a value for Hydra’s current acceleration of 3.23x10-14 mi/s2 . This amounts to 1.1706x10-10 ft/s2 . This value can be compared to the value of g at the surface of the Earth of approximately 32 ft/s2 , which is 2.73x1011 times larger.
It needs to be emphasized that A refers to a “residual acceleration.” It is the result of a nearly equal competition between gravitational forces and the inertial forces which originated in the Big Bang explosion. It is clear from eq. (3), however, that gravity is losing the battle at every stage. The acceleration A obviously causes the galaxy to slightly increase its speed, but as this happens, the value of A increases as well since it is always proportional to v. The changes are extremely small in all cases but they are always in the same direction, with the galaxies all heading farther out into space at an ever increasing rate. Moreover, it is clear that eq. (3) is perfectly consistent with the concept of an expanding universe. The farther out the galaxy, the faster it moves in every case. This combined motion preserves the constancy of H, at least over a relatively small period of time. This result is not surprising considering how eq. (3) has been derived.
Another key point about the derivation of eq. (3) is the assumption that A is constant. In one sense, this assumption is not strictly correct because the derivation leads to the conclusion that A varies in direct proportion to the speed of the galaxy v. Yet, in practice this means that A will decrease by only 1% for a galaxy that is 100 times closer to Earth than Hydra with a speed which is 100 times less than Hydra’s, that is, one whose value of L is 3.8x107 ly = 2.23x1020 mi. Surely, that amount of variation over this large range is commensurate with the above constancy assumption since Hydra’s current value of A is only 1.17x10-10 ft/s2 .
Another area in which eq. (3) can prove instructive is in resolving the question of the age of the universe. Since δv=Aδt, one can compute the value of the elapsed time δt relative to t=0 by considering the case at the present time when the speed of the galaxy (it doesn't matter which one because the formulas are applicable to all) is equal to v. Substitution of this value in eq. (3) then allows the amount of time since t=0 to be computed in order for the speed of the galaxy to have reached the current value of v:


In line with the assumptions made in the present model, it would be plausible to conclude that tx is the value of the time that has elapsed since the universe began with the Big Bang explosion. The main problem with this conclusion is that previous estimates for the age of the universe have tended to be around only 16 billion years (tu ). The latter amount of elapsed time is at least of the same order of magnitude as tx , but following through with the assumption that tu is the correct value for the age of the Universe shows that this interpretation is fraught with inconsistencies in the context of the present analysis, or at least aspects that are difficult to justify. It would mean, for example, that at time t=tu , the speeds of the galaxies were all roughly a fairly large fraction of 21/37, i.e. [(37-16)/37], of their current values. The corresponding distances would all be (21/37)2 smaller than they are today. It is clearly very difficult to explain that at the above assumed time of the Big Bang (t=tu ), the Hubble-type order of the galaxy system as a whole would be so clearly developed. Does one just ignore input t values that are less than 21 billion years in applying the model?
On the other hand, looking upon tx as the amount of time that has elapsed since the Big Bang explosion occurred requires considerably less discussion regarding the results of the model. In other words, in agreement with the general description on the effects involved, all the matter of the universe should have been in motion within nanoseconds of the explosion. At that time, so the argument goes, all the galaxies were just beginning their outward movement, that is, each with approximately v=0 at that point. Moreover, they were all centered at a single point in space (L=0). From then onward, the speeds of the galaxies increased in direct proportion to the elapsed time t since the Big Bang occurred at exactly t=0, while the corresponding distances relative to this origin increased in direct proportion to t2 , both of which trends are completely consistent with the (nearly) constant value of the acceleration A of the galaxies assumed in the present model.
The simple mathematical nature of the characteristics of constant acceleration can be used to good advantage in another important way. As motion of the galaxy proceeds, one can use the formulas to compute both the changes in its distance and speed, δv and δL, for a given amount of time δt, in terms of the present acceleration value A = v/tx from eq. (3):
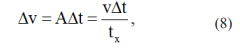
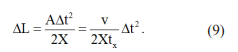
The factor X has been included in eq. (9) to account for any potential change in units. For example, if δL is to be given in ly, then X is the conversion factor required to change from ly to mi [see the definition after eq. (1)] when the speed v has the unit of mi/s (note that both tx and δt have the unit of s). Since δL/δv=L/v over at least a short period of elapsed time [see the discussion after eq. (1)], it follows that the corresponding change δH in the Hubble Constant is equal to δL/δv; hence, from eqs. (8) and (9) one obtains:
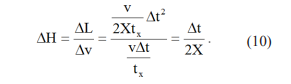
The concept of constant accelerations for the galaxies leads very easily to the results of eqs. (8) and (9) for the dependence of their speeds v and separations L from present-day Earth. In particular, v varies as the first power of δt and δL as the square thereof. Consequently, it comes as no surprise that the ratio of distance to speed, which is Hubble’s Constant, turns out to be directly proportional to δt.
The term “constant” for this quantity clearly refers to the fact that the value of the ratio is, at least to a good approximation, the same for all galaxies at the current time. What eq. (10) indicates, however, is that Hubble’s Constant is time-dependent and is definitely not constant in this respect. At the time of the Big Bang explosion (δt=0), for example, Hubble's Constant had a value of zero. In other words, if one goes backward in time, the distance L decreases faster than the corresponding value of v for each galaxy. The universe gradually shrinks as we look backward in time to the point at which the universe started. Their H=L/v ratio is also equal to zero at that point in time, as one can see by taking the limit of this quantity at t=0 in eq. (10). What does the future look like from this point of view? If 37 billion (tx ) more years pass, the speeds of each galaxy should double according to eq. (8), whereas their respective separations from the “origin of the universe (L=0)” given in eq. (9) will have all quadrupled relative to the present values, making the volume of the “spherical universe” 64 times larger than it is today. Of course, all this assumes that there will have been no cataclysmic event to affect the constant-acceleration assumption used to arrive at these equations. The value of the corresponding accelerations exhibited by each galaxy will also have doubled in each case, as indicated in eq. (4), because of their direct proportionality to the speed of each galaxy.
According to eq. (10), in between δt=tx and 2tx , H will simply change in direct proportion to the elapsed time that has occurred since t=0. Hubble's Constant is thus seen to be a clock of the universe. The amount of time since the Big Bang explosion can be evaluated to high accuracy simply by measuring the distances and speeds of the various galaxies and using this information to determine the then current value of Hubble’s Constant.
There are three main cosmological theories to explain the origin of the universe [1]. The steady-state theory certainly does not mesh well with all the evidence of a Big Bang explosion. The second assumes that the Big Bang not only occurred, but that its force continues to the present day to push the known galaxies farther into space, eventually taking them all the way to infinity, however that may be defined. The third theory assumes on the contrary that the universe is oscillating between explosion and collapse.
The latter theory is based in large part on belief in Einstein's theory of general relativity (GTR) which he introduced in 1916 [2]. According to Einstein, the gravitational pull on massive bodies can be expressed as a curvature of space [3]. His first ideas on this subject appear to go back to a paper he published in 1911 [4]. He felt that he could use his 1905 version of relativity theory (Special Relativity STR) to explain the apparent displacement of star images during solar eclipses [5]. This attempt gave a result for the angle in question which was only half as large as believed experimentally, but this error was removed in his GTR paper five years later. According to his biographer, Einstein realized he needed to know something about Riemannian geometry to carry out his program, and so he contacted his friend, Marcel Grossmann, in 1912 to obtain the necessary instruction [6]. This ultimately led to his 1916 paper on GTR and his successful calculation of the angle of light bending.
It is commonly believed in the astrophysical community that the only way to satisfactorily explain the displacement of star images and related phenomena is by way of GTR. Nothing could be further from the truth. In 1960 Schiff published a method which assumed that light travels in a perfectly straight line [7]. His method makes use of a conclusion that Einstein made about the speed of light in his 1907 paper [8] in which he enunciated the Equivalence Principle. He used his 1905 theory to claim that the speed of light decreases as it gets closer to a massive body such as the sun [5].
Einstein's conclusion was verified in 1964 by Shapiro in what the latter referred to as a “fourth test of general relativity [9].” Shapiro proved that radar pulses are indeed slowed when they pass close to planets. What Schiff showed with his paper is that light rays only appear to be bent by passing close to the sun. They each move at different speeds, however, becoming ever slower the closer they come to the sun. As a consequence, the wave front of the light rays is rotated. The angle of rotation is what experimentalists measure during solar eclipses.
In Schiff's view, the bending of light can easily be explained without making any assumptions about “curved space-time [7].” It should also be noted, however, that Schiff admitted that his method did not satisfactorily explain another key phenomenon, namely the advancement of the perihelion of Mercury’s orbit. This failure clearly detracted from the attempt to convince physicists that his method was a genuine competitor with GTR. In more recent studies, however, Schiff's method has been extended so that it has become applicable to the Mercury orbit as well, and with comparable accuracy as is obtained with GTR [10-13].
The latter work has gone largely unnoticed by the astronomical community, however. As a result, a great deal of credence is given to GTR, including to its famous cosmological predictions. It is claimed, for example, that the degree of curvature in space may be sufficient to cause the expansion of the universe to slow down and ultimately, if there is sufficient mass, even to reverse course. Once one sees that there is another way to quantitatively explain the key effects of the displacement of star images and the advancement of Mercury's perihelion, however, it becomes imperative to much more thoroughly scrutinize the predictions of GRT in this regard.
The great advantage of the present approach is that it makes no assumptions whatsoever based on either GRT or Schiff's method [2, 7]. Rather, it simply places the experimental fact of Hubble’s Constant in conjunction with the quantitative relations that one uses to describe the motion of ordinary objects that are under the influence of a constant acceleration. The results are shown in eqs. (3) and (8-10) for the galaxy separations, speeds and accelerations, respectively. This analysis shows that there is a steady compounding of the accelerations and speeds of the galaxies. The expression for the speed of each galaxy at any future time v(T) is conveniently given in terms of finite differences of elapsed time δt as follows:
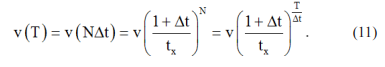
The quantity (1+δt/tx ) is positive definite. This result is closely akin to the conventional compound interest formula. It shows that the speed v (T) of any given galaxy grows exponentially, as well as does the corresponding acceleration value. It is completely incompatible with both the steady-state universe model as well as the oscillating universe prediction of GRT. The result is not dependent in any way on the value of the total mass of the universe, but is based instead entirely on the experimental evidence provided by measurements of the value of Hubble’s Constant. Gravitational and inertial forces are assumed to be in continuous competition with one another, but no concrete information regarding the strength of either is required to obtain the final results of the theory. It is clear, however, that the strength of the inertial forces always outweighs that of gravitation, in complete agreement with the expanding universe theory of cosmology
The fundamental cosmological question as to whether the universe is closed or open has been investigated with a simple formalism derived from elementary calculus. The information contained in observations which have led to the discovery of Hubble’s Constant has been combined with an assumption of nearly constant acceleration for the known galaxies. On this basis, relationships have been obtained which accurately describe the manner in which the speeds and separations of the various galaxies vary with time. In particular, it is found that the net accelerations of the galaxies vary only slightly over very long distances and are of exceptionally small magnitude. For example, that for Hydra is only 1.17x10-10 ft/s2 , 2.73x1011 times smaller than the acceleration due to gravity near the Earth's surface. It is clear that such small values must be the result of a close competition between the large gravitational forces acting on the various galaxies, on the one hand, and the inertial forces which have propelled them outward as a result of the tremendous explosion that is thought to have been responsible for the creation of the universe, on the other. The small values of the net acceleration serve as justification for the assumption of constant acceleration in deriving these results for speeds and separations of the various galaxies.
A key result of the analysis is that the galaxy acceleration is directly proportional to its speed. This leads to a “compounding effect” which causes the acceleration values to increase continuously as the corresponding speeds gradually increase. There is thus strong theoretical support for the view that the universe is not only expanding, but is doing so at an ever increasing (exponential) rate. It will take a cataclysmic event to stop this process, one that is certainly not expected from the laws of physics that have been observed over millennia of human investigation.
The relationships predicted between the separations of the galaxies and their corresponding speeds suggest further that Hubble's Constant itself is increasing in direct proportion to the amount of elapsed time that has occurred since the Big Bang explosion. One can therefore look upon Hubble's constant as a clock of the universe. Its current value of 100,000 (ly/mi/s) should double by the time a comparable amount of time has passed. During that period, the speeds of the individual galaxies are also expected to double, while their separations from laboratories on Earth should quadruple.
All of the above equations contain a constant which is an amount of time equal to tx = 37 billion years. This value is of the same order of magnitude as the amount of time tu = 16 billion years often given as the presumed age of the universe, but it is 2.5 times larger. The value of tx is directly proportional to Hubble’s Constant, so it is quite unlikely that such a large discrepancy can result from an inaccuracy in the latter value. This finding is perhaps an indication that the experimental assumptions that have led to the figure of 16 billion years are themselves deserving of further scrutiny. Consistent with this conclusion is the report on social media from Fermi lab that the quasar ULAS J1342 + 0928 has a “commoving distance” of approximately 29.36 billion ly from Earth. It also has been reported that the width of the universe is 96 billion ly, from which one can conclude that the universe is 48 billion ly.
