Author(s): <p>Metin Celalettin</p>
The ‘Celalettin-Field Quantum Observation Tunnel’ (Celalettin Tunnel) is a quantum observation technique. It is within a pneumatic manifold of Euclidean space where the randomness of particle Orbital Angular Momentum (OAM) is mitigated via electric polarization. It is described by the ‘Celalettin Tunnel Conjecture’.
‘Celalettin Tunnel Conjecture’ can be exploited to propose a paediatric ‘Magnetic Resonance Imaging’ (MRI) machine in pulmonary diagnostics for Severe Acute Respiratory Syndrome Coronavirus-2’ in paediatric patients to avoid the need to administer General Anaesthesia
In a two photon entangled system, if λIdler were held and λsig were directed through an IC-Manifold, a Celalettin Tunnel is theorized. Electric polarization effects the Orbital Angular Momentum (OAM) spin within the pneumatic matter inside the IC-Manifold. [1, 2].
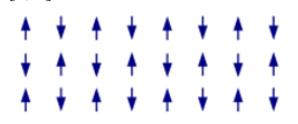
Figure 1: Antiferromagnetic ordering
The Celalettin Tunnel theoretically works similarly to Magnetic Resonance Imaging (MRI) [3, 4]. An entangled photon depolarizes the Helium-3 atoms as it burrows through the IC-Manifold and creates a tunnel [5]. The depolarized particles are considered a single quantum system and can be used to acquire information on the λsig [5-9]. λsig would become weaker as it scattered through an ensemble of atomic Helium-3 until it was absorbed or escaped [10-12].

Figure 2: Celalettin-Field quantum observation tunnel in an ICManifold (Helium-3 atoms in grey have been depolarized)
At Figure 2, the Celalettin Tunnel is made from the collective depolarized electrons in the IC-Manifold [3, 5, 13 & 14] immediately after the λsig penetrated it [5, 9, 15 & 16]. If a gas is subject to anti-ferromagnetism its intrinsic spin properties will polarize and portray entropy attributes such like a solid [4, 17 & 18]. Those affected atoms could emit a bound electron depending on the photon’s energy, given:

Where: ni = the density of atoms in the i-th state of ionization, that is with i electrons removed gi = the degeneracy of states for the i-ions ?i = the energy required to remove i electrons from a neutral atom, creating an i-level ion. ne = is the electron density λ = the thermal de Broglie wavelength of an electron
We use the classical models by considering the classical spins with magnetic moments µA 6= µB. To simplify we assume that nuclear spin interaction is disordered of the Heisenberg form [9, 22, 23 & 27]. So, the ferromagnetic model described by the classical Hamiltonian of the type:
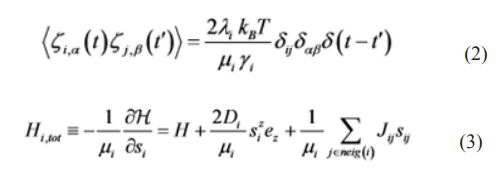
H = Hamiltonian N = Total number of spins I and J = Lattice sites Di = The anisotropy constant of site I Si = 1 The third sum is over neighbour pairs Jij = JAA(BB)>0 Heisenberg exchange interaction parameter λi = Is the coupling to the heat bath parameter a,B = Cartesian Z components heat bath and T is the temperature
Each point of an n-dimensional manifold has a neighbourhood or a set of points defining IC-Manifold boundaries [17, 24]. Helium-3 has an intrinsic nuclear spin of ½ and can be hyperpolarized by spin exchange optical pumping and is achieved by Coulomb Forces; such that:

Where: r = the distance between the two charges q and Q Newtons.
Given the Boltzmann equation to accommodate the density of the environment in which the photon-electron interactions will occur in the presence of an electric field:

ne = electron number density
Te = temperature of the plasma, and
kB = Boltzmann constant.
θ = work function
The Schrodinger wave function equation:

Where the Laplacian of a scalar for spherical coordinates is given by
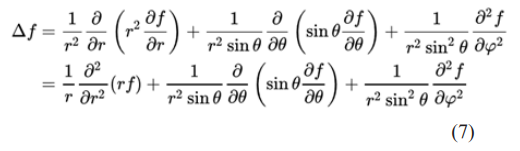
E = energy
V = potential energy
m = mass
h = Planck’s constant
θ = the azimuthal angle, and
θ = the zenith angle or co-latitude
Rearranged to express quantum entangled photons:

αe = eigenvalues
e = λsig
g = λidler
Bra-ket notation An electron’s spin: With an observer: obsobs For an entangled quantum system: (+)/2- (+)/2 Where the observer is added: obs(+)obs/2- obs(+)obs/2 If the observer can measure the state, then the state of the observer changes and the observer can no longer be factored out of the whole state: (obs1+obs2)/2-(obs1+obs2)/2. The quantumness of obs1≠obs2obs1≠obs2 describes the electron spin as not acting quantum mechanically and hence decoherence is achieved [25].
Spin exchange optical pumping can be represented by:
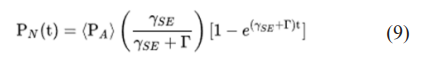
PN(t) = Nuclear polarization (spin)
is the atom’s polarization
λSE = the spin exchange rate
λ = the longitudinal relaxation rate
t = time it takes for polarized particle to return to random state
The Lagrangian scalar formulation to investigate the required kinetic energy of a photon to cause the Celalettin Tunnel [24]. It is given by:
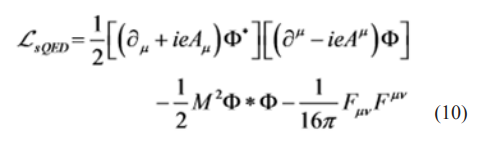
θ = charged scalar field,
θ* = its complex conjugate
The electromagnetic strength required is given by Faraday’s law of induction. The Euler-Lagrange equation describes the motion for the scalar field [1]:
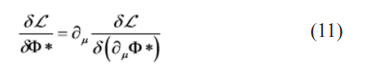
Yielding the Klein-Gordon [15]:

Where:
a and q are the quantum parameters.
IC-Manifold repolarization is expected to occur, given:

Mxy = the transverse component of the magnetization vector T2 = a time constant characterizing the signal decay e = Euler’s number
A ‘Celalettin Tunnel Conjecture’ can therefore mathematically be described:

TCelalettin is the Celalettin Tunnel
is the Schrodinger equation
Cen is the Mathieu differential equation
LQED symbolizes Lagrangian QED
PN(t) is the rate of nuclear spin repolarization
Paediatric patients are typically administered a GA when undergoing an MRI due to the requirement to stay still for extended periods. This is because of the manner in which the protons are circularly polarized. MRI developed from Nuclear Magnetic Resonance (NMR) uses the same phenomena to identify chemical structures based on a spectrum [1, 19, 27 & 28].
A technique; in vivo Magnetic Resonance (MR) spectrograph allows chemical identification on specific parts of the brain. Looking at whether the cells in a brain tumour contain alphahydroxy glutaric acid differentiates gliomas that have a mutation in the IDH1 or IDH2 gene for example. Pulse sequences to glean biochemical information non-invasively can be recalibrated for different patients [19, 27].
In an MRI, the flip angle is the rotation of the nuclear spin vector relative to the main magnetic field. To improve the signal with an MRI, the flip angle needs to be chosen using the Ernst angle. A 90° flip angle using the Ernst angle will yield the maximum signal intensity (or signal-to-noise ratio) per number of averaged Free Induction Decays (FID)s [3-5]. The flips are done over and over against while the patient stays still, and the average number of nuclear spin ensembles is taken to produce the image. This can involve the patient remaining still for up to five minutes.
This study explores whether a 180° flip angle could be achieved for a paediatric MRI by exploiting the ‘Celalettin Tunnel Conjecture’, rather than taking several measurements over the five to 10-minute imaging time experienced by the patient [3, 4 & 19]. It could produce a decisive image within seconds. In theory the number of FIDs required to produce the image would be reduced. This is because a 180° flip angle would be twice as effective as determining the different molecular make-up of different anatomy, and the number of images taken would be drastically reduced because of such [11, 12].
The brain is surrounded by cerebrospinal fluid (CSF), which has similar signal intensity on images as brain tissue. So there a pulse sequence called fluid attenuation inversion recovery (FLAIR) that makes hyperintense signals from water turn hypointense (black) on T2 images while keeping lesions hyperintense and recognisable [11]. This is the same as other tissues in the body; their FLAIR signals are too similar for a single quarter-second image, so multiple investigative techniques are required by the MRI to produce images [10, 11]. This weakness in extant MRI technologies causes paediatric patients to be administered a GA; a risk that medical practitioners claim outweighs the benefits of diagnostic techniques without an MRI [11, 12].
Imaging plays an important role in the management of COVID-19 patients. Typical CT features of COVID-19 pneumonia include multifocal bilateral Ground-glass opacity (GGO), with or without extant MRI patchy consolidations, prominent peripheral subpleural distribution, and posterior or lower lobe predilection. Similar signal intensity on images as brain tissue, pulmonary imaging diagnostics for COVID-19 are difficult to differentiate between like-diseases such as pneumonia. Even Influenza virus pneumonias show unilateral or bilateral ground-glass opacities with multifocal areas of consolidation [11, 12, 19 & 27].
Very few studies have shown CNS abnormalities related to COVID-19 on MRI. Herein, diagnostic imaging of SARS-CoV-2 brain lesions have produced some results. An initial rigorous assessment of pretest probability and imaging criteria should be introduced. Diagnostic scoring systems such as the Wells’ criteria, Pulmonary Embolism Rule-out Criteria (PERC), or the Geneva scoring system should be applied, before MRI [11, 27 & 28].
To create a T2-weighted image, magnetization is allowed to decay before measuring the MR signal by changing the echo time (TE). For a proposed T3-weighted image magnetization would not be allowed to decay, however a second electromagnetic field would be introduced. In 1920, Stern & Gerlac were able to point the nuclear spins of electrons in the same direction, while polarized.

They vaporized silver in an oven so silver atoms formed a beam that passed through a magnetic field in which it split in two. When electrons that have opposite spins are put together, there is no net magnetic field as they cancel each other out. Because electrons of the same spin cancel each other out, the one unpaired electron in the atom will determine the spin angle [27].
If a second electromagnetic field was utilized with magnetic moments harmonic to the magnetic moments of the first magnetic field, and in a direction which would pull the spin angles 180° prior to release, it would yield the maximum signal intensity per number of averaged FIDs. The longer.
In Equation (9), t, the time it takes for polarized particle to return to random state would take up to twice as long, enabling the MRI more time-related computational data and programmed criteria to meet which would produce a more effective medical image.
In an MRI, the flip angle is the rotation of the nuclear spin vector relative to the main magnetic field. To improve the signal with an MRI, the flip angle needs to be chosen using the Ernst angle:

A 90° flip angle using the Ernst angle will yield the maximum signal intensity (or signal-to-noise ratio) per number of averaged Free Induction Decays (FID)s. The flips are done over and over against while the patient stays still, and the average number of nuclear spin ensembles is taken to produce the image [1, 2 & 11]. This can involve the patient remaining still for up to five minutes.
If a 180° flip angle could be achieved, then rather than taking several measurements over the five-minute imaging time experienced by the patient, it could produce a decisive image one measurement [11, 12].
If the electron were pulled at a 180° flip angle in an MRI, then the patient would be exposed to a length of time of imaging in the diagnostic of ‘Severe Acute Respiratory Syndrome Coronavirus-2’ comparable to a handheld ultrasound or a CT. The electromagnetic strength required is given by Faraday’s law of induction. The trajectory of an ensemble of particles is derived from the Lagrange equations, where the Euler-Lagrange equation describes the motion for the scalar field [1].
Figure 6: ‘Severe Acute Respiratory Syndrome Coronavirus-2’ (COVID-19)
A paediatric patient suffering ‘Severe Acute Respiratory Syndrome Coronavirus-2’ (COVID-19). It infects and damages the type II alveolar cells of the lungs. Common symptoms include fever, cough, and shortness of breath. While chest CT is considered the modality of choice to diagnose pulmonary damage, such scans aren’t always as conclusive as an MRI [11].
As an alternative, bedside lung ultrasound is frequently used as a diagnostic. As the global infection rates of COVID-19 continue to rise, investigators in Italy evaluated whether lung ultrasound could be an effective tool in also identifying patients who have pneumonia specifically associated with the virus. The results weren’t significant. However, since its inception, the MRI has been the Rolls Royce of diagnostic imaging [3, 4, 5, 11 & 12].
For an adult, it would be unlikely that they would need an MRI as a CT scan would be sufficient, however in a paediatric patient where complications of COVID-19, pneumonia and other respiratory conditions, it may be too difficult to use these techniques. To determine whether ultrasound could feasibly be used to pinpoint COVID-19 pneumonia, researchers analysed 12 emergency department patients with the COVID-19 infection
These individuals received both lung ultrasound and CT. CT scans correlated strongly with the ultrasounds. 12 patients had groundglass opacity; five patients had a crazy-paving pattern. Scans identified a diffuse B-pattern with spared areas in all patients, and only three had posterior subpleural consolidations. The research showed that using a hand-held ultrasound was about as effective as a CT scan, where in the past, CT scans were the standard protocol for COVID-19 diagnostics [28].
While the Celalettin Tunnel Conjecture exploits antiferromagnetism to manipulate particle spin, it can be used on free electrons in paediatric patients, and if pulled at a 180° flip angle in an MRI, then the patient could be exposed to a length of time of imaging in the diagnostic of ‘Severe Acute Respiratory Syndrome Coronavirus-2’ comparable to a handheld ultrasound or a CT. This would avoid the need to administer General Anesthesia to paediatric patients undergoing pulmonary imaging for COVID-19 diagnostics [20, 21, 26].
